
【题目】已知函数![]() 是定义域在
是定义域在![]() 上的奇函数,且
上的奇函数,且![]() .
.
(1)用定义证明:函数![]() 在
在![]() 上是增函数,
上是增函数,
(2)若实数![]() 满足
满足![]() ,求实数
,求实数![]() 的范围.
的范围.
【答案】(1)证明见解析(2)![]()
【解析】
(1)根据![]() 求得
求得![]() ,根据单调性的定义,计算
,根据单调性的定义,计算![]() ,由此证得函数在
,由此证得函数在![]() 上为增函数.
上为增函数.
(2)利用函数的奇偶性化简![]() ,再利用函数的单调性结合函数的定义域列不等式组,解不等式组求得
,再利用函数的单调性结合函数的定义域列不等式组,解不等式组求得![]() 的取值范围.
的取值范围.
(1)∵函数![]() 是定义域为(-1,1)上的奇函数,
是定义域为(-1,1)上的奇函数,
∴f(0)=0,∴b=0,
∴![]()
任取x1,x2∈(-1,1),且x1<x2,
∴f(x1)-f(x2)=![]() -
-![]()
=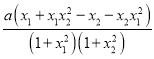 =
=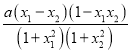 ,
,
∵a>0,-1<x1<x2<1,
∴x1-x2<0,1-x1x2>0,1+![]() >0,1+
>0,1+![]() >0,
>0,
∴函数f(x)在(-1,1)上是增函数.
(2)∵f(2t-1)+f(t-1)<0,∴f(2t-1)<-f(t-1),
∵函数![]() 是定义域为(-1,1)上的奇函数,且a>0.
是定义域为(-1,1)上的奇函数,且a>0.
∴f(2t-1)<f(1-t),
∵函数f(x)在(-1,1)上是增函数,
∴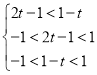 ,
,
解得![]() .
.
故实数t的范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】设![]() 是等差数列,
是等差数列,![]() 是各项都为正数的等比数列,且
是各项都为正数的等比数列,且![]() ,
,![]() .
.
(1)求![]() ,
,![]() 的通项公式;
的通项公式;
(2)设![]() ,
,![]() ,若
,若![]() ,
,![]() ,
,![]() 成等差数列(
成等差数列(![]() 、
、![]() 为正整数且
为正整数且![]() ),求
),求![]() 和
和![]() 的值;
的值;
(3)设![]() 为数列
为数列![]() 的前
的前![]() 项和,是否存在实数
项和,是否存在实数![]() ,使得
,使得![]() 对一切
对一切![]() 均成立?若存在,求出
均成立?若存在,求出![]() 的最大值;若不存在,说明理由.
的最大值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义域为R上的奇函数,当x>0时,f(x)=x2+2x.
(1)求f(x)的解析式;
(2)若不等式f(t﹣2)+f(2t+1)>0成立,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图1和图2中所有的正方形都全等,图1中的正方形放在图2中的①②③④某一位置,所组成的图形能围成正方体的概率是( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 1
D. 1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 过点
过点![]() ,其参数方程为
,其参数方程为![]() (
(![]() 为参数,
为参数,![]() ),以
),以![]() 为极点,
为极点,![]() 轴非负半轴为极轴,建立极坐标系,曲线
轴非负半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)求已知曲线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地通过市场调查得到西红柿种植成本![]() (单位:元/千克)与上市时间
(单位:元/千克)与上市时间![]() (单位:
(单位:![]() 天)的数据如下表:
天)的数据如下表:
时间 |
|
|
|
种植成本 |
|
|
|
(1)根据上表数据,发现二次函数能够比较准确描述![]() 与
与![]() 的变化关系,请求出函数的解析式;
的变化关系,请求出函数的解析式;
(2)利用选取的函数,求西红柿最低种植成本及此时的上市天数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 对任意实数x、y恒有
对任意实数x、y恒有![]() ,当x>0时,f(x)<0,且
,当x>0时,f(x)<0,且![]() .
.
(1)判断![]() 的奇偶性;
的奇偶性;
(2)求![]() 在区间[-3,3]上的最大值;
在区间[-3,3]上的最大值;
(3)若![]() 对所有的
对所有的![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,
,![]() .
.
(1)当![]() 时,若对任意
时,若对任意![]() 均有
均有![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(2)设直线![]() 与曲线
与曲线![]() 和曲线
和曲线![]() 相切,切点分别为
相切,切点分别为![]() ,
,![]() ,其中
,其中![]() .
.
①求证:![]() ;
;
②当![]() 时,关于
时,关于![]() 的不等式
的不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com