
分析 (I)利用互化公式即可得出.
(Ⅱ)设P(2cosθ,sinθ),可得S=|PA|2+|PB|2+|PC|2+|PD|2=20+12cos2θ,即可得出.
解答 解:(Ⅰ)点A,B,C,D的直角坐标分别为A($\sqrt{3}$,1),B(-$\sqrt{3}$,1),
C(-$\sqrt{3}$,-1),D($\sqrt{3}$,-1).
(Ⅱ)设P(2cosθ,sinθ),令S=|PA|2+|PB|2+|PC|2+|PD|2,
则S=16cos2θ+4sin2θ+16=20+12cos2θ,∵0≤cos2θ≤1,∴S的取值范围是[20,32].
点评 本题考查了极坐标化为直角坐标、两点之间距离公式、三角函数的单调性与值域,考查了推理能力与计算能力,属于中档题.


 单元期中期末卷系列答案
单元期中期末卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
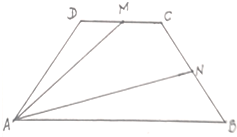 如图,在底角为45°的等腰梯形ABCD中,$\overrightarrow{AB}$=3$\overrightarrow{DC}$,M,N分别为CD,BC的中点.设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$.
如图,在底角为45°的等腰梯形ABCD中,$\overrightarrow{AB}$=3$\overrightarrow{DC}$,M,N分别为CD,BC的中点.设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
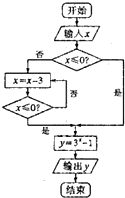
| A. | 0 | B. | $-\frac{2}{3}$ | C. | $-\frac{8}{9}$ | D. | $-\frac{26}{27}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分但不必要条件 | B. | 充分且必要条件 | ||
| C. | 必要但不充分条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com