
①截y轴所得弦长为2;
②被x轴分成两段圆弧,其弧长的比为3∶1.
在满足条件①②的所有圆中,求圆心到直线l:x-2y=0的距离最小的圆的方程.
思路分析:可设所求圆的标准方程为(x-a)2+(y-b)2=r2,它有三个待定系数a、b、r.将条件②等价转化为所截圆弧所对的圆心角的度数为90°,进而可求出r与b的关系.将条件①等价转化为r与a的关系.最后利用算术平均值不等式或方程有实数解的条件:判别式不小于0等方法求出a、b、r.
解法一:设圆的圆心坐标为P(a,b),半径为r,
则点P到x轴、y轴的距离分别为|b|、|a|.
由题设知圆P截x轴所得劣弧的圆心角为90°,
于是圆P截x轴所得弦长为![]() r,
r,
故r2=2b2.
又圆P截y轴所得的弦长为2,
所以有r2=a2+1,
从而得2b2-a2=1.
点P(a,b)到直线x-2y=0的距离为d=![]() .
.
所以5d2=|a-2b|2=a2+4b2-4ab=2a2+2b2-4ab+1=2(a-b)2+1≥1,
当且仅当a=b时,上式取等号,
此时5d2=1,从而d取得最小值.
由此有
解此方程组得![]()
由r2=2b2,知r2=2.
故所求圆的方程是(x-1)2+(y-1)2=2或(x+1)2+(y+1)2=2.
解法二:同解法一得d=![]() ,
,
故a-2b=±![]() d.
d.
于是a2=4b2±![]() bd+5d2,①
bd+5d2,①
将a2=2b2-1代入①式,
整理得2b2±![]() db+5d2+1=0.②
db+5d2+1=0.②
把它看作关于b的一元二次方程,由于方程有实根,
故判别式非负,
于是Δ=8(5d2-1)≥0,
解得5d2≥1.
所以5d2有最小值1,从而d有最小值![]() .
.
将其代入②式得2b2±4b+2=0,
解得b=±1.
将b=±1代入r2=2b2,得r2=2.
又由r2=a2+1,得a=±1.
综上,解得a=±1,b=±1,r2=2.
由|a-2b|=1,知a、b同号.
于是,所求圆的方程是(x-1)2+(y-1)2=2或(x+1)2+(y+1)2=2.
绿色通道:解题的过程就是实现条件向结论转化的过程.对于直线与圆,需要综合平面几何、解析几何、代数知识,将条件转化成熟悉的形式,以便用常规的解题思路求解.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
| QM |
| QP |
查看答案和解析>>
科目:高中数学 来源: 题型:
 在A、B、C、D四小题中只能选做2题,每小题10分,共计20分,请在答题纸指定区域内作答,解答应写出文字说明、证明过程或演算步骤.
在A、B、C、D四小题中只能选做2题,每小题10分,共计20分,请在答题纸指定区域内作答,解答应写出文字说明、证明过程或演算步骤.1 1 |
| 2 |
| π |
| 4 |
|
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
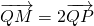 的点M的轨迹为曲线C.
的点M的轨迹为曲线C.查看答案和解析>>
科目:高中数学 来源:2011年湖北省黄冈市高考数学交流试卷3(文科)(解析版) 题型:解答题
 的点M的轨迹为曲线C.
的点M的轨迹为曲线C.查看答案和解析>>
科目:高中数学 来源:2011年湖北省黄冈市高考数学交流试卷(文科)(解析版) 题型:解答题
 的点M的轨迹为曲线C.
的点M的轨迹为曲线C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com