
【题目】已知圆O:x2+y2=1过椭圆C: ![]() (a>b>0)的短轴端点,P,Q分别是圆O与椭圆C上任意两点,且线段PQ长度的最大值为3. (Ⅰ)求椭圆C的方程;
(a>b>0)的短轴端点,P,Q分别是圆O与椭圆C上任意两点,且线段PQ长度的最大值为3. (Ⅰ)求椭圆C的方程;
(Ⅱ)过点(0,t)作圆O的一条切线交椭圆C于M,N两点,求△OMN的面积的最大值.
【答案】解:(Ⅰ)∵圆O过椭圆C的短轴端点,∴b=1, 又∵线段PQ长度的最大值为3,
∴a+1=3,即a=2,
∴椭圆C的标准方程为 ![]() .
.
(Ⅱ)由题意可设切线MN的方程为y=kx+t,即kx﹣y+t=0,则 ![]() ,得k2=t2﹣1.①
,得k2=t2﹣1.①
联立得方程组 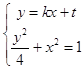 ,消去y整理得(k2+4)x2+2ktx+t2﹣4=0.
,消去y整理得(k2+4)x2+2ktx+t2﹣4=0.
其中△=(2kt)2﹣4(k2+4)(t2﹣4)=﹣16t2+16k2+64=48>0,
设M(x1 , y1),N(x2 , y2),则 ![]() ,
, ![]() ,
,
则 ![]() .②
.②
将①代入②得 ![]() ,∴
,∴ ![]() ,
,
而 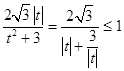 ,等号成立当且仅当
,等号成立当且仅当 ![]() ,即
,即 ![]() .
.
综上可知:(S△OMN)max=1
【解析】(Ⅰ)由圆O过椭圆C的短轴端点b=1,线段PQ长度的最大值为3,a+1=3,a=2,即可求得椭圆方程;(Ⅱ)设直线MN的方程,由点到直线的距离公式,求得k2=t2﹣1,代入椭圆方程,由韦达定理及弦长公式求得丨MN丨,利用三角形的面积公式及基本不等式的性质,即可求得△OMN的面积的最大值.


科目:高中数学 来源: 题型:
【题目】某重点中学为了解高一年级学生身体发育情况,对全校700名高一年级学生按性别进行分层抽样检查,测得身高(单位:cm)频数分布表如表1、表2. 表1:男生身高频数分布表
身高(cm) | [160,165) | [165,170) | [170,175) | [175,180) | [180,185) | [185,190) |
频数 | 2 | 5 | 14 | 13 | 4 | 2 |
表2:女生身高频数分布表
身高(cm) | [150,155) | [155,160) | [160,165) | [165,170) | [170,175) | [175,180) |
频数 | 1 | 7 | 12 | 6 | 3 | 1 |
(1)求该校高一女生的人数;
(2)估计该校学生身高在[165,180)的概率;
(3)以样本频率为概率,现从高一年级的男生和女生中分别选出1人,设X表示身高在[165,180)学生的人数,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入a,b的值分别是21,28,则输出a的值为( ) 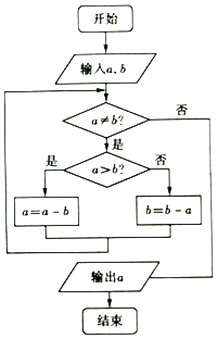
A.14
B.7
C.1
D.0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an}和{bn}中,a1= ![]() ,{an}的前n项为Sn , 满足Sn+1+(
,{an}的前n项为Sn , 满足Sn+1+( ![]() )n+1=Sn+(
)n+1=Sn+( ![]() )n(n∈N*),bn=(2n+1)an , {bn}的前n项和为Tn .
)n(n∈N*),bn=(2n+1)an , {bn}的前n项和为Tn .
(1)求数列{bn}的通项公式bn以及Tn .
(2)若T1+T3 , mT2 , 3(T2+T3)成等差数列,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数f(x)= ![]() sin2x﹣
sin2x﹣ ![]() cos2x+1的图象向左平移
cos2x+1的图象向左平移 ![]() 个单位,再向下平移1个单位,得到函数y=g(x)的图象,则下列关予函数y=g(x)的说法错误的是( )
个单位,再向下平移1个单位,得到函数y=g(x)的图象,则下列关予函数y=g(x)的说法错误的是( )
A.函数y=g(x)的最小正周期为π
B.函数y=g(x)的图象的一条对称轴为直线x= ![]()
C.![]() g(x)dx=
g(x)dx= ![]()
D.函数y=g(x)在区间[ ![]() ,
, ![]() ]上单调递减
]上单调递减
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() (a,b∈R,且a≠0,e为自然对数的底数).
(a,b∈R,且a≠0,e为自然对数的底数).
(I)若曲线f(x)在点(e,f(e))处的切线斜率为0,且f(x)有极小值,求实数a的取值范围.
(II)(i)当 a=b=l 时,证明:xf(x)+2<0;
(ii)当 a=1,b=﹣1 时,若不等式:xf(x)>e+m(x﹣1)在区间(1,+∞)内恒成立,求实数m的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在(0,+∞)上的函数f(x)满足f′(x)+2f(x)= ![]() ,且f(1)=
,且f(1)= ![]() ,则不等式f(lnx)>f(3)的解集为( )
,则不等式f(lnx)>f(3)的解集为( )
A.(﹣∞,e3)
B.(0,e3)
C.(1,e3)
D.(e3 , +∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com