
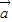 、
、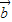 是两个不共线的非零向量 (t∈R)
是两个不共线的非零向量 (t∈R)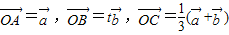 ,那么当实数t为何值时,A、B、C三点共线?
,那么当实数t为何值时,A、B、C三点共线?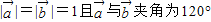 ,那么实数x为何值时
,那么实数x为何值时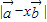 的值最小?
的值最小?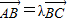 ,由此等式建立起关于λ,t的方程求出t的值;
,由此等式建立起关于λ,t的方程求出t的值;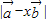 表示成关于实数x的函数,根据所得的函数判断出它取出最小值时的x的值.
表示成关于实数x的函数,根据所得的函数判断出它取出最小值时的x的值.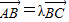 ,则有
,则有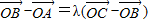
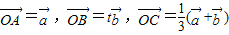
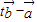 =
= ,又
,又 、
、 是两个不共线的非零向量
是两个不共线的非零向量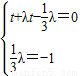 解得
解得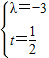
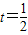 时,A、B、C三点共线
时,A、B、C三点共线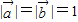 且
且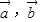 两向量的夹角是120°
两向量的夹角是120°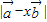 2=
2= =1+x+x2=(x+
=1+x+x2=(x+ )2+
)2+
 时,
时,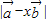 的值最小为
的值最小为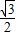


科目:高中数学 来源:河北省沙河市高一数学单元测试(4) 题型:解答题
(本题满分12分)
设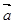 、
、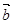 是两个不共线的非零向量(
是两个不共线的非零向量(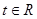 ).
).
(I)记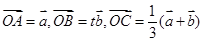 ,那么当实数t为何值时,A、B、C三点共线?
,那么当实数t为何值时,A、B、C三点共线?
(II)若 ,那么实数x为何值时
,那么实数x为何值时 的值最小?
的值最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
设![]() 、
、![]() 是两个不共线的非零向量(t∈R).
是两个不共线的非零向量(t∈R).
(1)记![]() =
=![]() ,
,![]() =
=![]() ,
,![]() =
=![]() ,那么当实数
,那么当实数![]() 为何值时,
为何值时,![]() 三点共线?
三点共线?
(2)若![]() =
=![]() =1且
=1且![]() 与
与![]() 夹角为120°,那么实数
夹角为120°,那么实数![]() 为何值时,
为何值时,![]() 的值最小?
的值最小?
查看答案和解析>>
科目:高中数学 来源:2009-2010学年度新课标高一下学期数学单元测试4-平面向量与三角恒等变换 题型:解答题
设 、
、 是两个不共线的非零向量(
是两个不共线的非零向量(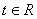 ).
).
(I)记 ,那么当实数t为何值时,A、B、C三点共线?
,那么当实数t为何值时,A、B、C三点共线?
(II)若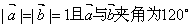 ,那么实数x为何值时
,那么实数x为何值时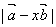 的值最小?
的值最小?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com