
分析 (1)利用f(-4)=f(4),代入解析式求值;
(2)设x<0,则-x>0,得到f(-x),利用函数为偶函数,得到x<0时的解析式,最后表示R上的解析式.
解答 解:(1)∵f(-4)=f(4)=$lo{g}_{\frac{1}{2}}4=-lo{g}_{2}4$=-2,
(2)当x<0时,-x>0,
则f(-x)=$lo{g}_{\frac{1}{2}}(-x)$,
∵函数f(x)是偶函数,
∴f(-x)=f(x),
∴f (x)=log${\;}_{\frac{1}{2}}$ (-x).
∴函数f(x)的解析式为f(x)=$\left\{\begin{array}{l}{lo{g}_{\frac{1}{2}}x,x>0}\\{0,x=0}\\{lo{g}_{\frac{1}{2}}(-x),x<0}\end{array}\right.$.
点评 本题考查了函数的性质运用;关键是利用已知函数为偶函数将所求转化为已知解析式的自变量范围内.


 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届湖南永州市高三高考一模考试数学(文)试卷(解析版) 题型:选择题
已知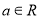 ,“
,“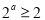 ”是“函数
”是“函数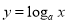 在
在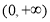 上为减函数”的( )
上为减函数”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
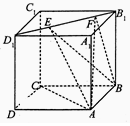 如图,正方体ABCD-A1B1C1D1的棱长为2,线段D1B1上有两个动点E、F,且EF=1,则下列结论中错误的是( )
如图,正方体ABCD-A1B1C1D1的棱长为2,线段D1B1上有两个动点E、F,且EF=1,则下列结论中错误的是( )| A. | AC⊥BE | B. | AA1∥平面BEF | ||
| C. | 三棱锥A-BEF的体积为定值 | D. | △AEF的面积和△BEF的面积相等 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,7] | B. | [2,7] | C. | [-2,14] | D. | [2,14] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com