若函数y=f(x)是周期为2的偶函数,当x∈[2,3]时,f(x)=x-1.在y=f(x)的图象上有两点A、B,它们的纵坐标相等,横坐标都在区间[1,3]上,定点C的坐标为(0,a)(其中2<a<3),
(1)求当x∈[1,2]时,f(x)的解析式;
(2)定点C的坐标为(0,a)(其中2<a<3),求△ABC面积的最大值.
解:(1)∵f(x)是以2为周期的周期函数,
当x∈[2,3]时,f(x)=x-1,
∴当x∈[0,1]时,f(x)=f(x+2)=(x+2)-1=x+1.…(1分)
∵f(x)是偶函数,
∴当x∈[-1,0]时,f(x)=f(-x)=-x+1,…(2分)
当x∈[1,2]时,f(x)=f(x-2)=-(x-2)+1=-x+3.…(4分)
(2)设A、B的横坐标分别为3-t,t+1,1≤t≤2,
则|AB|=(t+1)-(3-t)=2t-2,…(6分)
∴△ABC的面积为S=

(2t-2)•(a-t)
=-t
2+(a+1)t-a(1≤t≤2)
=-(t-

)
2+
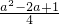
,
∵2<a<3,∴

<

<2.
当t=

时,S
最大值=
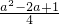
.…(12分)
分析:(1)由f(x)是以2为周期的周期函数,当x∈[2,3]时,f(x)=x-1,知当x∈[0,1]时,f(x)=f(x+2)=(x+2)-1=x+1.由f(x)是偶函数,知当x∈[-1,0]时,f(x)=f(-x)=-x+1.由此能求出当x∈[1,2]时,f(x)的解析式.
(2)设A、B的横坐标分别为3-t,t+1,1≤t≤2,则|AB|=(t+1)-(3-t)=2t-2,故△ABC的面积为S=

(2t-2)•(a-t)=-(t-

)
2+
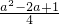
,由此能求出S
最大值.
点评:本题考查二次函数的性质和应用,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.

 (2t-2)•(a-t)
(2t-2)•(a-t) )2+
)2+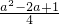 ,
, <
< <2.
<2. 时,S最大值=
时,S最大值=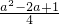 .…(12分)
.…(12分) (2t-2)•(a-t)=-(t-
(2t-2)•(a-t)=-(t- )2+
)2+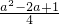 ,由此能求出S最大值.
,由此能求出S最大值.
