
(Ⅰ)求证BC⊥SC;
(Ⅱ)求面ASD与面BSC所成二面角的大小;
(Ⅲ)设棱SA的中点为M,求异面直线DM与SB所成角的大小.

17.本小题主要考查直线与平面的位置关系等基本知识,考查空间想象能力、逻辑思维能力和运算能力..
(Ⅰ)证法一:如图1,

图1
∵底面ABCD是正方形,
∴BC⊥DC.
∵SD⊥底面ABCD,
∴DC是SC在平面ABCD上的射影,由三垂线定理得BC⊥SC.
证法二:如图1,
∵底面ABCD是正方形,
∴BC⊥DC.
∵SD⊥底面ABCD,
∴SD⊥BC,又DC∩SD=D,
∴BC⊥平面SDC,
∴BC⊥SC.
(Ⅱ)解法一:
∵SD⊥底面ABCD,且ABCD为正方形,
∴可以把四棱锥S-ABCD补形为长方体A1B1C1S—ABCD,如图2.
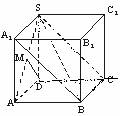
图2
面ASD与面BSC所成的二面角就是面ADSA1与面BCSA1所成的二面角.
∵SC⊥BC,BC∥A1S,
∴SC⊥A1S,
又SD⊥A1S,
∴∠CSD为所求二面角的平面角.
在Rt△SCB中,由勾股定理得SC=![]() ,
,
在Rt△SDC中,由勾股定理得SD=1.
∴∠CSD=45°.
即面ASD与面BSC所成二面角的大小为45°.
解法二:如图3,
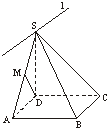
图3
过点S作直线l∥AD,
∴l在面ASD上,
∵底面ABCD为正方形,
∴l∥AD∥BC,
∴l在面BSC上,
∴l为面ASD与面BSC的交线.
∵SD⊥AD,BC⊥SC,
∴l⊥SD,l⊥SC,
∴∠CSD为面ASD与面BSC所成二面角的平面角.
(以下同解法一)
(Ⅲ)解法一:如图3,
∵SD=AD=1,∠SDA=90°,
∴△SDA是等腰直角三角形.
又M是斜边SA的中点,
∴DM⊥SA.
∵BA⊥AD,BA⊥SD,AD∩SD=D,
∴BA⊥面ASD,SA是SB在面ASD上的射影.
由三垂线定理得DM⊥SB.
∴异面直线DM与SB所成的角为90°.
解法二:如图4,
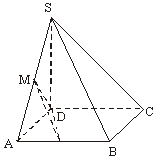
图4
取AB中点P,连结MP,DP.
在△ABS中,由中位线定理得
MP∥SB,
∴∠DMP是异面直线DM与SB所成的角.
∵MP=![]() SB=
SB=![]() ,
,
又DM=![]() ,DP=
,DP=![]() =
=![]() ,
,
∴在△DMP中,有DP2=MP2+DM2,
∴∠DMP=90°.
∴异面直线DM与SB所成的角为90°.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
 如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的一点,平面EDC⊥平面SBC.
如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的一点,平面EDC⊥平面SBC.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,四棱锥S-ABCD的底面是边长为3的正方形,SD丄底面ABCD,SB=3
如图,四棱锥S-ABCD的底面是边长为3的正方形,SD丄底面ABCD,SB=3| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•醴陵市模拟)如图,四棱锥S-ABCD的底面是矩形,SA⊥底面ABCD,P为BC边的中点,AD=2,AB=1.SP与平面ABCD所成角为
(2013•醴陵市模拟)如图,四棱锥S-ABCD的底面是矩形,SA⊥底面ABCD,P为BC边的中点,AD=2,AB=1.SP与平面ABCD所成角为| π | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,四棱锥S-ABCD底面ABCD是正方形,SA⊥底面ABCD,E是SC上一点,且SE=2EC,SA=6,AB=2.
如图,四棱锥S-ABCD底面ABCD是正方形,SA⊥底面ABCD,E是SC上一点,且SE=2EC,SA=6,AB=2.查看答案和解析>>
科目:高中数学 来源: 题型:
 (2006•西城区二模)如图,四棱锥S-ABCD中,平面SAC与底面ABCD垂直,侧棱SA、SB、SC与底面ABCD所成的角均为45°,AD∥BC,且AB=BC=2AD.
(2006•西城区二模)如图,四棱锥S-ABCD中,平面SAC与底面ABCD垂直,侧棱SA、SB、SC与底面ABCD所成的角均为45°,AD∥BC,且AB=BC=2AD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com