
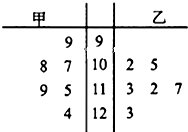
 在数学趣味知识培训活动中,甲、乙两名学生的6次培训成绩如茎叶图所示:
在数学趣味知识培训活动中,甲、乙两名学生的6次培训成绩如茎叶图所示:. |
| x甲 |
| 99+107+108+115+119+124 |
| 6 |
. |
| x乙 |
| 102+105+112+113+117+123 |
| 6 |
| 1 |
| 6 |
| 206 |
| 3 |
| 1 |
| 6 |
| 148 |
| 3 |
. |
| x甲 |
. |
| x乙 |
| ||
|
| 2 |
| 5 |
| ||||
|
| 8 |
| 15 |
| ||
|
| 1 |
| 15 |
| ξ | 0 | 1 | 2 | ||||||
| P |
|
|
|
| 2 |
| 5 |
| 8 |
| 15 |
| 1 |
| 15 |
| 2 |
| 3 |


科目:高中数学 来源: 题型:
| A、402 | B、403 |
| C、404 | D、405 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 某工厂有25周岁以上(含2S周岁)工人300名,25周岁以下工人200名为研究工人的日平均生产量是否与年龄有关,现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组,再将两组工人的日平均生产件数分成5组:[50,60),[60,70),[70,80),[80,90),[90,100),分别加以统计,得到如图所示的频率分布直方图.
某工厂有25周岁以上(含2S周岁)工人300名,25周岁以下工人200名为研究工人的日平均生产量是否与年龄有关,现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组,再将两组工人的日平均生产件数分成5组:[50,60),[60,70),[70,80),[80,90),[90,100),分别加以统计,得到如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| OA |
| OB |
| OP |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、{x|x<-1} |
| B、{x|0<x<1} |
| C、{x|x<-1或0<x<1} |
| D、{x|x≥1或-1<x<0} |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| S1 |
| 1 |
| S2 |
| 1 |
| Sn |
| m-2010 |
| 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com