
分析 由于二次函数的对称轴为x=-a,分①当-a<-1、②当-1≤-a<$\frac{1}{2}$、③当$\frac{1}{2}$≤-a≤2、④当-a>2四种情况,分别利用二次函数的性质求得函数的最值
解答 解:∵函数f(x)=x2+2ax+1=(x+a)2+1-a2 的对称轴为x=-a,
①当-a<-1,即a>1时,函数y在[-1,2]上是增函数,
故当x=-1时,函数y取得最小值为2-2a;当x=2时,函数y取得最大值为5+4a.
②当-1≤-a<$\frac{1}{2}$,即$\frac{1}{2}$<a≤1时,x=-a时,函数y取得最小值为1-a2;
当x=2时,函数y取得最大值为5+4a.
③当$\frac{1}{2}$≤-a≤2,即-2≤a≤-$\frac{1}{2}$时,x=-a时,函数y取得最小值为1-a2;
当x=-1时,函数y取得最大值为2-2a.
④当-a>2,即a<-2时,函数y在[-1,2]上是减函数,
故当x=-1时,函数y取得最大值为2-2a;
当x=2时,函数y取得最小值为5+4a
点评 本题主要考查求二次函数在闭区间上的最值,二次函数的性质的应用,体现了分类讨论的数学思想,关键是根据对称轴与区间的关系判断得出分类的标准,属于中档题


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
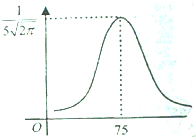 某市高二理科学生数学考试的成绩x服从正态分布,其密度函数为f(x)=$\frac{1}{\sqrt{2π}σ}$e${\;}^{\frac{(x-μ)^{2}}{2{σ}^{2}}}$,密度曲线如图,已知该市理科学生总数是10000人,则成绩位于(65,85]的人数约是9544.
某市高二理科学生数学考试的成绩x服从正态分布,其密度函数为f(x)=$\frac{1}{\sqrt{2π}σ}$e${\;}^{\frac{(x-μ)^{2}}{2{σ}^{2}}}$,密度曲线如图,已知该市理科学生总数是10000人,则成绩位于(65,85]的人数约是9544.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 68.26% | B. | 95.44% | C. | 99.74% | D. | 31.74% |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com