
| 1 | 1+x2 |
| 1 | ||
1+
|
| 1 | ||
1+
|
| ||||
(1+
|
| (x1+x2)(x2-x1) | ||||
(1+
|
| x | 2 1 |
| x | 2 2 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
设函数f(x)的定义域为R,当x<0时f(x)>1,且对任意的实数x,y∈R,有![]()
(Ⅰ)求f(0),判断并证明函数f(x)的单调性;
(Ⅱ)数列![]() 满足
满足![]() ,且
,且![]() ,数列
,数列![]() 满足
满足![]() w.w.w.k.s.5.u.c.o.m
w.w.w.k.s.5.u.c.o.m ![]()
①求数列![]() 通项公式。
通项公式。
②求数列![]() 的前n项和Tn的最小值及相应的n的值.
的前n项和Tn的最小值及相应的n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
![]()
(北京市西城外语学校·2010届高三测试)设函数f(x)的定义域为R,当x<0时f(x)>1,且对任意的实数x,y∈R,有![]()
(Ⅰ)求f(0),判断并证明函数f(x)的单调性;
(Ⅱ)数列![]() 满足
满足![]() ,且
,且![]() ,数列
,数列![]() 满足
满足![]()
①求数列![]() 通项公式。
通项公式。
②求数列![]() 的前n项和Tn的最小值及相应的n的值.
的前n项和Tn的最小值及相应的n的值.
查看答案和解析>>
科目:高中数学 来源:2015届内蒙古高一上学期期中考试数学试卷(解析版) 题型:解答题
18. 已知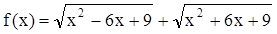
(1)画函数f(x)的图像 .(2)求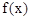 的单调区间.
的单调区间.
(3)求函数f(x)的定义域,值域.
(4)判断并证明函数f(x)的奇偶性.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com