
如图,三棱锥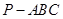 中,
中,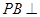 底面
底面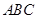 于
于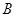 ,
,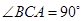 ,
,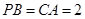 ,点
,点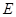 是
是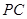 的中点.
的中点.

(1)求证:侧面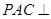 平面
平面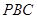 ;
;
(2)若异面直线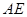 与
与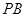 所成的角为
所成的角为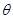 ,且
,且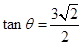 ,
,
求二面角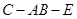 的大小.
的大小.
(1)对于线面垂直的证明,主要是利用判定定理,然后结合这个条件来得到面面垂直的证明。
(2)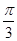
【解析】
试题分析:解:(1)∵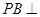 底面
底面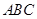 ,
, 平面
平面 ,
,
∴ 平面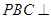 平面
平面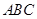 , 又∵
, 又∵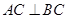 ,
,
平面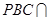 平面
平面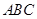
 , ∴
, ∴  平面
平面 3分
3分
而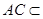 平面
平面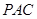 ∴侧面
∴侧面 平面
平面 .
5分
.
5分
(2)取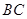 的中点
的中点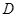 ,则
,则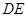 是
是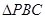 的中位线
的中位线
故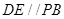 ,所以
,所以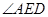 就是异面直线
就是异面直线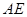 与
与 所成的角
所成的角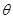 , 7分
, 7分
设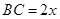 ,则在
,则在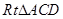 中,
中,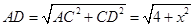 ,
,
在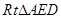 中,
中,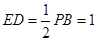 ,∴
,∴ 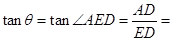
 ,
,
而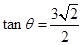 ,∴
,∴  ,即
,即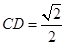 .
9分
.
9分
过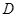 作
作 于点
于点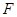 ,连
,连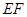 . ∵
. ∵
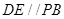 ,
,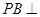 底面
底面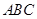
∴ 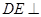 底面
底面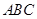 ,从而
,从而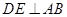 ,又∵
,又∵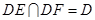 ,
,
∴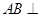 平面
平面 ,从而
,从而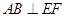 ,
,
所以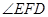 就是二面角
就是二面角 的平面角. 11分
的平面角. 11分
由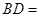
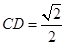 ,得
,得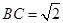 ,
由
,
由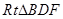 ∽
∽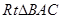 ,
,
可得 ,即
,即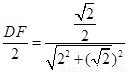 解得
解得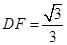 ,
,
在 中,
中, ,所以
,所以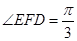 ,
,
故二面角 的大小为
的大小为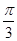 .
14分
.
14分
解法2:如图,以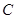 为原点,以
为原点,以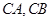 分别为
分别为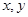 轴建立直角坐标系.
轴建立直角坐标系.

设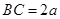 ,则
,则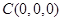 ,
,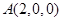 ,
,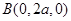 ,
,
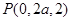 ,从而
,从而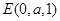 .
.
∴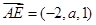 ,
, , 7分
, 7分
∵异面直线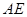 与
与 所成的角为
所成的角为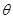 ,且
,且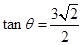 ,
,
∴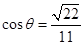 ,
,
又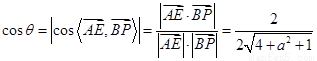 ,
,
从而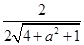
 ,解得
,解得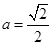 ...
9分
...
9分
∴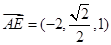 ,
,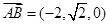 ,
, ,
,
设平面 的法向量为
的法向量为 ,则由
,则由
得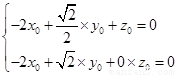 , 令
, 令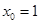 ,得
,得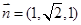 .
11分
.
11分
又平面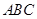 的法向量为
的法向量为 , 12分
, 12分
∴
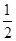 ,∴
,∴  ,
,
所以二面角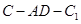 的大小为
的大小为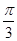 .
14分
.
14分
考点:面面垂直,二面角
点评:主要是考查了空间几何体中垂直的证明以及异面直线的角和二面角的平面角的借助于向量来求解,属于中档题。


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源: 题型:
如图:三棱锥![]() 中,
中,![]() ^底面
^底面![]() ,若底面
,若底面![]() 是边长为2的正三角形,且
是边长为2的正三角形,且![]() 与底面
与底面![]() 所成的角为
所成的角为![]() .若
.若![]() 是
是![]() 的中点,求:
的中点,求:
(1)三棱锥![]() 的体积;
的体积;
|

(2)异面直线![]() 与
与![]() 所成角的大小(结果用反三角函数值表示).
所成角的大小(结果用反三角函数值表示).
查看答案和解析>>
科目:高中数学 来源:2014届浙江省温州八校高三9月期初联考理科数学试卷(解析版) 题型:解答题
如图,三棱锥 中,
中, 底面
底面 ,
, ,
, ,
, 为
为 的中点,点
的中点,点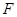 在
在 上,且
上,且 .
.

(Ⅰ)求证:平面 平面
平面 ;
;
(Ⅱ)求平面 与平面
与平面 所成的二面角的平面角(锐角)的余弦值.
所成的二面角的平面角(锐角)的余弦值.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年上海市青浦区高三上学期期终学习质量调研测试数学试卷 题型:解答题
(本题满分12分) 本题共有2个小题,第1小题满分6分,第2小题满分6分.
如图:三棱锥 中,
中, ^底面
^底面 ,若底面
,若底面 是边长为2的正三角形,且
是边长为2的正三角形,且
与底面 所成的角为
所成的角为 ,若
,若 是
是 的中点,
的中点,
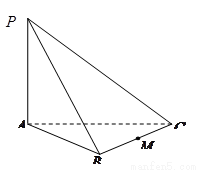
求:(1)三棱锥 的体积;
的体积;
(2)异面直线 与
与 所成角的大小(结果用反三角函数值表示).
所成角的大小(结果用反三角函数值表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com