
已知函数y=x3-3mx2-4n3(mn≠0),过原点作函数图象的一条切线,切点A恰好是函数的极值点.
(1)讨论函数的单调性;
(2)证明:m+n=0.
(3)记f(x)=x3-3mx2-4n3(m<0),当x∈[-1,1]时,总有f(x)>-1,求m的取值范围.
解:(1)先求导,得y′=3x2-6mx, 令y′=0,得x=0,或x=2m.
则根据题意可知,点A的坐标为(0,0)或(2m,0).
当点A的坐标为(0,0)时,将点A的坐标代入y=x3-3mx2-4n3得n=0,
与mn≠0矛盾, 所以, x=0舍去.
由已知,m≠0.
当m<0时,函数在(-∞,2m),(0,+∞)内单调递增;在(2m,0)单调递减 .
当m>0时,函数在(-∞,0),(2m,+∞)内单调递增;在(0,2m)内单调递减.
(2)证明:由(1)可知,点A(2m,0)在函数的图象上,
∴0=(2m)3-3m?(2m)-4n3,
∴m3=-n3,
∴m+n=0.
(3)由(2)可得, f(x)=x3-3mx2+4m3, ∴f(-1)=-1-3m+4m3,
由(1)可知,当m<0时,在(0,1]内,函数f(x)单调递增,点(0,4m3)为函数的极小值点,
当x∈[-1,1]时,总有f(x)>-1当且仅当
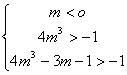
解得, -![]() <m<0.
<m<0.


 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com