
已知直线 (
( 为参数),曲线
为参数),曲线 (
( 为参数).
为参数).
(1)设 与
与 相交于
相交于 两点,求
两点,求 ;
;
(2)若把曲线 上各点的横坐标压缩为原来的
上各点的横坐标压缩为原来的 倍,纵坐标压缩为原来的
倍,纵坐标压缩为原来的 倍,得到曲线
倍,得到曲线 ,设点
,设点 是曲线
是曲线 上的一个动点,求它到直线
上的一个动点,求它到直线 的距离的最小值.
的距离的最小值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2017届江西新余一中高三上学期开学考试数学(文)试卷(解析版) 题型:解答题
已知函数 .
.
(1)试讨论函数 的单调性;
的单调性;
(2)若不等式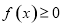 在区间
在区间 上恒成立, 求
上恒成立, 求 的取值范围, 并证明:
的取值范围, 并证明:
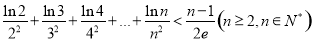 .
.
查看答案和解析>>
科目:高中数学 来源:2016届云南玉溪市高三第三次教学质检数学(文)试卷(解析版) 题型:选择题
已知三棱锥 的外接球为球
的外接球为球 ,球
,球 的直径
的直径 ,且
,且 都是等边三角形,则三棱锥
都是等边三角形,则三棱锥 的体积是( )
的体积是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2016届云南玉溪市高三第三次教学质检数学(文)试卷(解析版) 题型:选择题
已知 为异面直线,
为异面直线, 为两个不同的平面,
为两个不同的平面, ,直线
,直线 满足
满足 ,则( )
,则( )
A. 且
且 B.
B. 且
且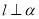
C. 且
且 D.
D.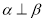 且
且
查看答案和解析>>
科目:高中数学 来源:2017届湖南长沙长郡中学高三入学考试数学(文)试卷(解析版) 题型:解答题
如图,在四棱锥 中,
中, 平面
平面 ,
, ,
, ,
, .
.
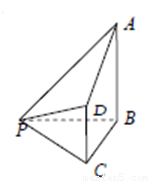
(1)求点 到平面
到平面 的距离;
的距离;
(2)点 为线段
为线段 上一点(含端点),设直线
上一点(含端点),设直线 与平面
与平面 所成角为
所成角为 ,求
,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2017届湖南长沙长郡中学高三入学考试数学(理)试卷(解析版) 题型:解答题
某城市城镇化改革过程中最近五年居民生活用水量逐年上升,下表是2011年至2015年的统计数据:
年份 | 2011 | 2012 | 2013 | 2014 | 2015 |
居民生活用水量(万吨) | 236 | 246 | 257 | 276 | 286 |
(1)利用所给数据求年居民生活用水量与年份之间的回归方程 ;
;
(2)根据改革方案,预计在2020年底城镇改革结束,到时候居民的生活用水量将趋于稳定,预测该城市2023年的居民生活用水量.
参考公式: ,
, .
.
查看答案和解析>>
科目:高中数学 来源:2016届北京通州区高三4月一模数学(文)试卷(解析版) 题型:解答题
如图,在四棱锥 ,
, 底面正方形
底面正方形 ,
, 为侧棱
为侧棱 的中点,
的中点,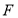 为
为 的中点,
的中点,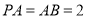 .
.
(Ⅰ)求四棱锥 体积;
体积;
(Ⅱ)证明: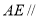 平面
平面 ;
;
(Ⅲ)证明:平面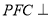 平面
平面 .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com