
分析 (1)利用定义法求数列{an}的通项公式.
(2)利用定义法求数列{bn}的通项公式,设F(n)=anbn+2=2-$\frac{1}{n+2}$-$\frac{1}{(n+2)^{2}}$,显然,F(n)在n∈N*单调递增.结合函数单调性求实数M的取值范围.
解答 解:(1)∵2Sn=(n+1)an+n-1,①
∴2Sn-1=nan-1+n-2,②.
由①-②得:2an=(n+1)an+nan-1+1,③
∴2an+1=(n+2)an+(n+1)an+1+1,④
由④-③得:nan-1+nan+1=2nan即an-1+an+1=2an,
∴数列{an}是等差数列.
又∵2S2=3a1+1,a1=2,
∴a2=3,d=1,
∴an=n+1;
(2)∵$\frac{{a}_{1}}{\sqrt{{b}_{1}+1}}$+$\frac{{a}_{2}}{\sqrt{{b}_{2}+1}}$+…+$\frac{{a}_{n}}{\sqrt{{b}_{n}+1}}$=$\frac{{n}^{2}+n}{2}$(n∈N*),①
∴$\frac{{a}_{1}}{\sqrt{{b}_{1}+1}}$+$\frac{{a}_{2}}{\sqrt{{b}_{2}+1}}$+…+$\frac{{a}_{n-1}}{\sqrt{{b}_{n-1}+1}}$=$\frac{(n-1)^{2}+n-1}{2}$(n∈N*),②
由①-②得:$\frac{{a}_{n}}{\sqrt{{b}_{n}+1}}$=$\frac{{n}^{2}+n}{2}$-$\frac{(n-1)^{2}+n-1}{2}$=n⇒bn=$\frac{2n+1}{{n}^{2}}$(n∈N*).
即F(n)=anbn+2=$\frac{(n+1)(2n+5)}{(n+2)^{2}}$=$\frac{2{n}^{2}+7n+5}{(n+2)^{2}}$=$\frac{2(n+2)^{2}-(n+2)-1}{(n+2)^{2}}$=2-$\frac{1}{n+2}$-$\frac{1}{(n+2)^{2}}$,
显然,F(n)在n∈N*单调递增.
∴F(n)≥F(1)=$\frac{14}{9}$,
∴M≤$\frac{14}{9}$.
点评 本题目主要考查了利用数列的递推公式求解数列的通项公式,解题中要注意等比数列的通差公式的应用.


科目:高中数学 来源: 题型:选择题
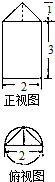 一个圆柱与一个三棱锥的组合体的正视图和俯视图如图所示,则该几何体的侧视图的面积为( )
一个圆柱与一个三棱锥的组合体的正视图和俯视图如图所示,则该几何体的侧视图的面积为( )| A. | 6 | B. | $\frac{13}{2}$ | C. | 7 | D. | 4π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{9}$ | C. | $\frac{1}{36}$ | D. | $\frac{25}{36}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第二象限角或第三象限的角 | B. | 第一象限角或第四象限的角 | ||
| C. | 第三象限角或第四象限的角 | D. | 终边在直线y=-x左下方的角 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
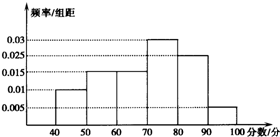 从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如图所示,观察图形,回答下列问题:
从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如图所示,观察图形,回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
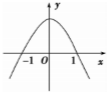 已知函数f(x)=ax3+bx2+cx在点x0处取得极小值-4,其导函数的图象经过(-1,0),(1,0),如图所示:
已知函数f(x)=ax3+bx2+cx在点x0处取得极小值-4,其导函数的图象经过(-1,0),(1,0),如图所示:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com