
分析 (1)通过点(n,$\frac{{S}_{n}}{n}$)(n∈N*)均在函数$y=\frac{1}{2}x+\frac{1}{2}$的图象上,求出Sn=$\frac{1}{2}$n2+$\frac{1}{2}$n,利用当n≥2时,an=Sn-Sn-1,求出通项公式;
(2)${b_n}=\frac{1}{{{a_n}•{a_{n+1}}}}$=$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$,利用裂项求和,Tn<$\frac{m}{20}$求得m的取值范围,即可求得使得Tn<$\frac{m}{20}$对所有n∈N*都成立的最小正整数m.
解答 解:(1)∵点$(n,\frac{S_n}{n}),\;(n∈{N^*})$均在函数$y=\frac{1}{2}x+\frac{1}{2}$的图象上,即$\frac{{S}_{n}}{n}$=$\frac{1}{2}$n+$\frac{1}{2}$,
∴Sn=$\frac{1}{2}$n2+$\frac{1}{2}$n,
当n≥2时,Sn-1=$\frac{1}{2}$(n-1)2+$\frac{1}{2}$(n-1),
an=Sn-Sn-1=$\frac{1}{2}$n2+$\frac{1}{2}$n-[$\frac{1}{2}$(n-1)2+$\frac{1}{2}$(n-1)]=n,
当n=1时,a1=1,满足an=1,
即数列{an}的通项公式为an=n;
(2)${b_n}=\frac{1}{{{a_n}•{a_{n+1}}}}$=$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$,
数列{bn}的前n项和Tn,Tn=(1-$\frac{1}{2}$)+($\frac{1}{2}$-$\frac{1}{3}$)+($\frac{1}{3}$-$\frac{1}{4}$)+…+($\frac{1}{n}$-$\frac{1}{n+1}$),
=1-$\frac{1}{n+1}$,
=$\frac{n}{n+1}$,
要使得Tn<$\frac{m}{20}$对所有n∈N*都成立,
则$\frac{m}{20}$≥1
∴m≥20,
即m的最小正整数m=20.
点评 本题考查数列的求和的方法,考查“裂项法”的应用,考查数列与不等式的综合应用,考查计算能力,属于中档题.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{3}π,3π$ | B. | $4\sqrt{3}π,3π$ | C. | $\sqrt{3}π,2π$ | D. | 3π,2π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
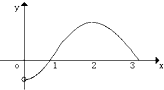 已知函数f(x)是定义在(-3,0)∪(0,3)上的偶函数,当0<x<3时,f(x)的图象如图所示,则不等式f(-x)•x>0的解集是( )
已知函数f(x)是定义在(-3,0)∪(0,3)上的偶函数,当0<x<3时,f(x)的图象如图所示,则不等式f(-x)•x>0的解集是( )| A. | (-1,0)∪(0,1) | B. | (-3,-1)∪(1,3) | C. | (-3,-1)∪(0,1) | D. | (-1,0)∪(1,3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com