
 某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[90,100),[100,110),…,[140,150)后得到如下部分频率分布直方.观察图形的信息,回答下列问题:
某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[90,100),[100,110),…,[140,150)后得到如下部分频率分布直方.观察图形的信息,回答下列问题:分析 (1)由频率分布直方图,能求出分数在[120,130)内的频率,并能补全这个频率分布直方图.
(2)由频率分布直方图能估计本次考试的平均分及中位数.
(3)用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本,则分数段为[110,120)中抽取的学生数为2人,分数段为[120,130)中抽取的学生数为4人,从中任取2个,基本事件总数n=${C}_{6}^{2}=15$,至多有1人在分数段[120,130)内包含的基本事件为:m=${C}_{6}^{2}-{C}_{4}^{2}$=9,由此能求出至多有1人在分数段[120,130)内的概率.
解答 解:(1)由频率分布直方图,得:
分数在[120,130)内的频率为:1-(0.010+0.015+0.015+0.025+0.005)×10=0.3.
$\frac{频率}{组距}$=$\frac{0.3}{10}$=0.03,补全后的直方图如右图所示.
(2)由频率分布直方图得:
平均分为:95×0.010×10+105×0.015×10+115×0.015×10+125×0.030×10+135×0.025×10+×0.005×10=121.
∵[90,120)的频率为(0.010+0.015+0.015)×10=0.4,
[120,130)的频率为:0.030×10=0.3,
∴中位数为:120+$\frac{0.5-0.4}{0.3}×10$=$\frac{370}{3}$.
(3)用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本,
则分数段为[110,120)中抽取的学生数为:$\frac{0.015}{0.015+0.030}$×6=2人,
分数段为[120,130)中抽取的学生数为:$\frac{0.030}{0.015+0.030}×6$=4人,
将该样本看成一个总体,从中任取2个,基本事件总数n=${C}_{6}^{2}=15$,
至多有1人在分数段[120,130)内包含的基本事件为:m=${C}_{6}^{2}-{C}_{4}^{2}$=9,
∴至多有1人在分数段[120,130)内的概率P(A)=$\frac{m}{n}$=$\frac{9}{15}$=$\frac{3}{5}$.
点评 本题考查频率分布直方图的应用,考查概率的求法,考查频率分布直方图、分层抽样、概率等基础知识,考查数据处理能力、运算求解能力,考查数形结合思想,是基础题.


科目:高中数学 来源: 题型:解答题
 2017年高考特别强调了要增加对数学文化的考查,为此瓦房店市高级中学高三年级数学组特命制了一套与数学文化有关的专题训练卷(文、理科试卷满分均为100分),并对整个高三年级的学生进行了测试.现从这些学生中随机抽取了50名学生的成绩,按照成绩为[50,60),[60,70),…,[90,100]分成了5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分).
2017年高考特别强调了要增加对数学文化的考查,为此瓦房店市高级中学高三年级数学组特命制了一套与数学文化有关的专题训练卷(文、理科试卷满分均为100分),并对整个高三年级的学生进行了测试.现从这些学生中随机抽取了50名学生的成绩,按照成绩为[50,60),[60,70),…,[90,100]分成了5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
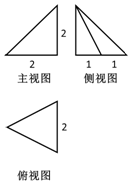
| A. | $\frac{4}{3}$ | B. | $7+\sqrt{5}$ | C. | $5+\sqrt{5}$ | D. | $7+2\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{9}$ | D. | $\frac{4}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com