
已知P为椭圆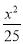 +
+ =1上的一点,M,N分别为圆(x+3)2+y2=1和圆(x-3)2+y2=4上的点,则|PM|+|PN|的最小值为________.
=1上的一点,M,N分别为圆(x+3)2+y2=1和圆(x-3)2+y2=4上的点,则|PM|+|PN|的最小值为________.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2015高考数学(理)一轮配套特训:9-1随机抽样(解析版) 题型:选择题
某卫星将在某时落在地球的某个地方,砸中地球人的概率约为 ,为了研究中学生对这件事情的看法,某中学对此事进行了问卷调查,共收到2000份有效问卷,得到如下结果.
,为了研究中学生对这件事情的看法,某中学对此事进行了问卷调查,共收到2000份有效问卷,得到如下结果.
对卫星撞地 球的态度 | 关注但 不担心 | 关注有 点担心 | 关注且非 常担心 | 不关注 |
人数(人) | 1000 | 500 | x | 300 |
则从收到的2000份有效问卷中,采用分层抽样的方法抽取20份,抽到关注且非常担心的问卷份数为( )
A.2 B.3 C.5 D.10
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-7抛物线(解析版) 题型:选择题
直线4kx-4y-k=0与抛物线y2=x交于A、B两点,若|AB|=4,则弦AB的中点到直线x+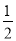 =0的距离等于( )
=0的距离等于( )
A. B.2 C.
B.2 C.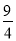 D.4
D.4
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-6双曲线(解析版) 题型:选择题
已知双曲线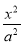 -
-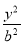 =1(a>0,b>0)的离心率为2,一个焦点与抛物线y2=16x的焦点相同,则双曲线的方程为( )
=1(a>0,b>0)的离心率为2,一个焦点与抛物线y2=16x的焦点相同,则双曲线的方程为( )
A.-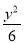 =1 B.
=1 B.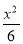 -
-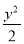 =1
=1
C.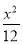 -
-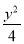 =1 D.
=1 D.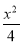 -
-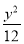 =1
=1
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-5椭圆(解析版) 题型:选择题
过点M(-2,0)的直线l与椭圆x2+2y2=2交于P1,P2,线段P1P2的中点为P.设直线l的斜率为k1(k1≠0),直线OP(O为坐标原点)的斜率为k2,则k1k2等于( )
A.-2 B.2 C.- D.
D.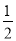
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-5椭圆(解析版) 题型:选择题
椭圆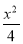 +y2=1的两个焦点为F1,F2,过F1作垂直于x轴的直线与椭圆相交,一个交点为P,则|PF2|=( )
+y2=1的两个焦点为F1,F2,过F1作垂直于x轴的直线与椭圆相交,一个交点为P,则|PF2|=( )
A. B.
B.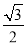 C.
C.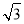 D.4
D.4
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-4直线与圆、圆与圆的位置关系(解析版) 题型:解答题
已知圆C:x2+(y-1)2=5,直线l:mx-y+1-m=0,且直线l与圆C交于A、B两点.
(1)若|AB|=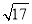 ,求直线l的倾斜角;
,求直线l的倾斜角;
(2)若点P(1,1)满足2 =
=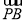 ,求此时直线l的方程.
,求此时直线l的方程.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-3圆的方程(解析版) 题型:解答题
已知直线l:2x+y+2=0及圆C:x2+y2=2y.
(1)求垂直于直线l且与圆C相切的直线l′的方程;
(2)过直线l上的动点P作圆C的一条切线,设切点为T,求|PT|的最小值.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-1直线的倾斜角与斜率、直线方程(解析版) 题型:选择题
直线ax+by+c=0同时要经过第一、第二、第四象限,则a,b,c应满足( )
A.ab>0,bc<0 B.ab>0,bc>0
C.ab<0,bc>0 D.ab<0,bc<0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com