
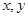 满足约束条件:
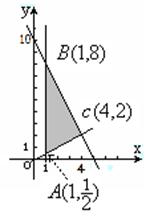
满足约束条件: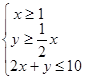 的可行域为
的可行域为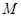
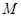 (用阴影表示,并注明边界的交点或直线);
(用阴影表示,并注明边界的交点或直线);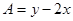 的最大值与
的最大值与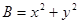 的最小值;
的最小值;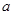 ,使函数
,使函数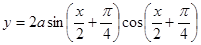 的图象经过区域
的图象经过区域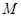 中的点,
中的点,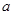 的取值范围.
的取值范围.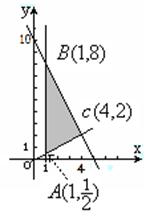
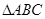 ; 2)
; 2)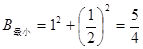 . 3)
. 3)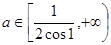 .
.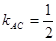
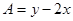 ∴
∴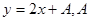 是
是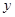 轴的截距,
轴的截距,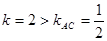
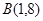 时,
时,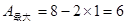
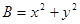 是表示区域M上的点
是表示区域M上的点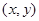 到原点O
到原点O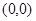 距离的平方.
距离的平方.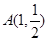 使所求距离的平方最小,∴
使所求距离的平方最小,∴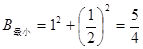
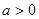
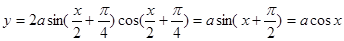 ]
]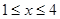
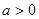 ,函数
,函数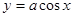 图象过点
图象过点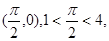
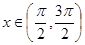 时,
时,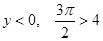
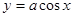 过区域M中的点,只须图象与射线
过区域M中的点,只须图象与射线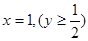 有公共点.
有公共点.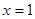 时,
时, 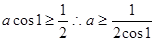
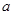 的取值范围是
的取值范围是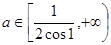
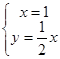 ,得
,得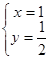 ∴
∴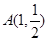
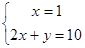 ,得
,得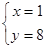 ∴
∴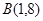
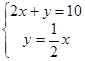 ,得
,得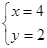 ∴
∴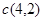
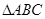
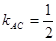
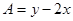 ∴
∴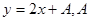 是
是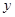 轴的截距,
轴的截距,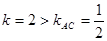
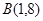 时,
时,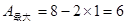
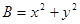 是表示区域M上的点
是表示区域M上的点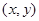 到原点O
到原点O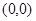 距离的平方.
距离的平方.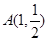 使所求距离的平方最小,∴
使所求距离的平方最小,∴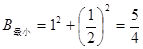 .
.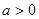
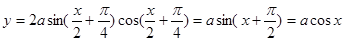
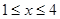
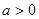 ,函数
,函数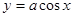 图象过点
图象过点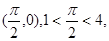
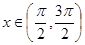 时,
时,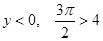
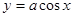 过区域M中的点,只须图象与射线
过区域M中的点,只须图象与射线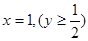 有公共点.
有公共点.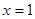 时,
时, 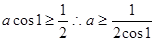
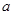 的取值范围是
的取值范围是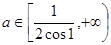 .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:单选题
| A.2000元 | B.2200元 | C.2400元 | D.2800元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com