
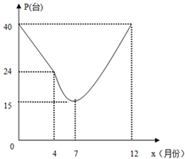
 ���ڹ����ص���ֽ��ܻ�����ҵ��ij�ֽ��ܲ�Ʒ���г����ۻ�ů��ij�������������ֲ�Ʒ���������������ǩ��������ͬ��Լ��һ���ڽ���Ϊ0.1��Ԫ/̨��һ���ʵ����������P��̨�����´�x֮�������ͼ��ʾ������ϵ��4�µ�12�½��Ʒ��϶��κ�����ϵ����
���ڹ����ص���ֽ��ܻ�����ҵ��ij�ֽ��ܲ�Ʒ���г����ۻ�ů��ij�������������ֲ�Ʒ���������������ǩ��������ͬ��Լ��һ���ڽ���Ϊ0.1��Ԫ/̨��һ���ʵ����������P��̨�����´�x֮�������ͼ��ʾ������ϵ��4�µ�12�½��Ʒ��϶��κ�����ϵ����
|



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
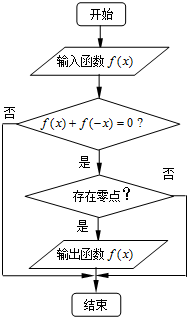 ij������ͼ��ʾ���������ĸ����������������ĺ����ǣ�������
ij������ͼ��ʾ���������ĸ����������������ĺ����ǣ�������| A��f��x��=x2 | ||
B��f(x)=
| ||
| C��f��x��=lnx+2x-6 | ||
| D��f��x��=x3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
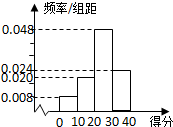 �Լס������������˶�Ա�ֱ���100�������еĵ÷��������ͳ�ƣ������ĵ÷�Ƶ�ʷֲ�ֱ��ͼ��ͼ���г��ҵĵ÷�ͳ�Ʊ����£�
�Լס������������˶�Ա�ֱ���100�������еĵ÷��������ͳ�ƣ������ĵ÷�Ƶ�ʷֲ�ֱ��ͼ��ͼ���г��ҵĵ÷�ͳ�Ʊ����£�| ��ֵ | [0��10�� | [10��20�� | [20��30�� | [30��40�� |
| ���� | 10 | 20 | 40 | 30 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| n2 |
| 4 |
| 1 |
| 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
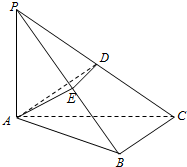 ��ͼ��������P-ABC�У�PA��ƽ��ABC��AP=AB=2
��ͼ��������P-ABC�У�PA��ƽ��ABC��AP=AB=2| 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
A��
| ||||||
B��
| ||||||
C��
| ||||||
D��
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com