
| n2 |
| 4 |
| 1 |
| 4 |
|
| 1 |
| 3 |
| 2n-1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 3 |
| n2 |
| 4 |
| 1 |
| 4 |
| n2 |
| 4 |
| (n-1)2 |
| 4 |
| 2n-1 |
| 4 |
| 2n-1 |
| 4 |
| 1 |
| 4 |
| 2n-1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2n-1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 3 |
|
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 3 |


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在Rt△AOB中,∠OAB=
如图,在Rt△AOB中,∠OAB=| π |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
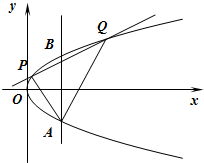 如图,两条相交线段AB、PQ的四个端点都在抛物线y2=x上,其中,直线AB的方程为x=m,直线PQ的方程为y=
如图,两条相交线段AB、PQ的四个端点都在抛物线y2=x上,其中,直线AB的方程为x=m,直线PQ的方程为y=| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
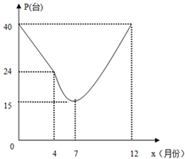 由于国家重点扶持节能环保产业,某种节能产品的市场销售回暖.某经销商销售这种产品,年初与生产厂家签订进货合同,约定一年内进价为0.1万元/台.一年后,实际月销售量P(台)与月次x之间存在如图所示函数关系(4月到12月近似符合二次函数关系).
由于国家重点扶持节能环保产业,某种节能产品的市场销售回暖.某经销商销售这种产品,年初与生产厂家签订进货合同,约定一年内进价为0.1万元/台.一年后,实际月销售量P(台)与月次x之间存在如图所示函数关系(4月到12月近似符合二次函数关系).查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com