
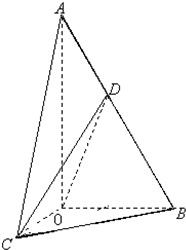
 如图,在Rt△AOB中,∠OAB=
如图,在Rt△AOB中,∠OAB=| π |
| 6 |
| OC |
| OD |
| 2 |
| OD |
| 1 |
| 2 |
| CO2+OE2 |
| 5 |
| 1 |
| 2 |
| 3 |
| CE2+DE2 |
| 2 |
| DE |
| CD |
| ||
2
|
| ||
| 4 |
| ||
| 4 |
| OC |
| OD |
| 2 |
| OD |
| OA•OB |
| AB |
| 3 |
| 2 | ||
|
2
| ||
| 3 |
2
| ||
| 3 |


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:高中数学 来源: 题型:
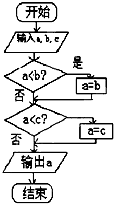
| A、求输出a,b,c三数的最大数 |
| B、求输出a,b,c三数的最小数 |
| C、将a,b,c按从小到大排列 |
| D、将a,b,c按从大到小排列 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| x1+x2 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
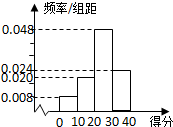 对甲、乙两名篮球运动员分别在100场比赛中的得分情况进行统计,做出甲的得分频率分布直方图如图,列出乙的得分统计表如下:
对甲、乙两名篮球运动员分别在100场比赛中的得分情况进行统计,做出甲的得分频率分布直方图如图,列出乙的得分统计表如下:| 分值 | [0,10) | [10,20) | [20,30) | [30,40) |
| 场数 | 10 | 20 | 40 | 30 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| n2 |
| 4 |
| 1 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
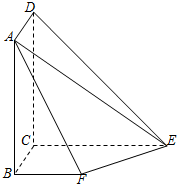 如图所示,平面ABCD⊥平面BCEF,且四边形ABCD为矩形,四边形BCEF为直角梯形,BF∥CE,BC⊥CE,DC=CE=4,BC=BF=2.
如图所示,平面ABCD⊥平面BCEF,且四边形ABCD为矩形,四边形BCEF为直角梯形,BF∥CE,BC⊥CE,DC=CE=4,BC=BF=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com