
【题目】如图,三棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 的中点,点
的中点,点![]() 在
在![]() 上,
上,![]() .
.
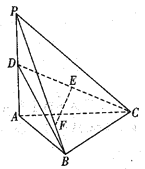
(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sin(2x﹣ ![]() ),x∈R.
),x∈R. 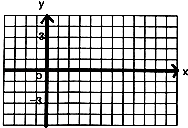
(1)在给定的平面直角坐标系中,画函数f(x)=2sin(2x﹣ ![]() ),x∈[0,π]的简图;
),x∈[0,π]的简图;
(2)求f(x)=2sin(2x﹣ ![]() ),x∈[﹣π,0]的单调增区间;
),x∈[﹣π,0]的单调增区间;
(3)函数g(x)=2cos2x的图象只经过怎样的平移变换就可得到f(x)=2sin(2x﹣ ![]() ),x∈R的图象?
),x∈R的图象?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,圆
,圆![]() ,圆心
,圆心![]() 到抛物线准线的距离为3,点
到抛物线准线的距离为3,点![]() 是抛物线在第一象限上的点,过点
是抛物线在第一象限上的点,过点![]() 作圆
作圆![]() 的两条切线,分别与
的两条切线,分别与![]() 轴交于
轴交于![]() 两点.
两点.
(1)求抛物线![]() 的方程;
的方程;
(2)求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,椭圆
,椭圆 ![]() 的离心率为
的离心率为![]() 是椭圆
是椭圆![]() 的右焦点,直线
的右焦点,直线![]() 的斜率为
的斜率为![]() 为坐标原点.
为坐标原点.
(1)求![]() 的方程;
的方程;
(2)设过点![]() 的动直线
的动直线![]() 与
与![]() 相交于
相交于![]() 两点,当
两点,当![]() 的面积最大时,求
的面积最大时,求![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过直角坐标平面xOy中的抛物线y2=2px(p>0)的焦点F作一条倾斜角为![]() 的直线与抛物线相交于A,B两点.
的直线与抛物线相交于A,B两点.
(1)用p表示线段AB的长;
(2)若![]() ,求这个抛物线的方程.
,求这个抛物线的方程.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1,F2为椭圆C: ![]() 的左右焦点,点
的左右焦点,点![]() 为其上一点,且有
为其上一点,且有![]() .
.
(1)求椭圆C的标准方程;
(2)圆O是以F1,F2为直径的圆,直线l: y =k x + m与圆O相切,并与椭圆C交于不同的两点A,B,若![]() ,求k的值.
,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某品牌手机厂商推出新款的旗舰机型,并在某地区跟踪调查得到这款手机上市时间(x个月)和市场占有率(y%)的几组相关对应数据:
x | 1 | 2 | 3 | 4 | 5 |
y | 0.02 | 0.05 | 0.1 | 0.15 | 0.18 |
(1)根据上表中的数据,用最小二乘法求出y关于x的线性回归方程;
(2)根据上述回归方程,分析该款旗舰机型市场占有率的变化趋势,并预测自上市起经过多少个月,该款旗舰机型市场占有率能超过0.5%(精确到月).
附:  ,
, ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com