
【题目】如图所示, ![]() 矩形
矩形![]() 所在的平面,
所在的平面, ![]() 分别是
分别是![]() 的中点.
的中点.
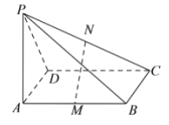
(1)求证: ![]() 平面
平面![]() ;
;
(2)求证: ![]() .
.
(3)当![]() 满足什么条件时,能使
满足什么条件时,能使![]() 平面
平面![]() 成立?并证明你的结论.
成立?并证明你的结论.
【答案】(1)见解析;(2)见解析;(3)当![]() 满足
满足![]() 时,能使
时,能使![]() 平面
平面![]() 成立.证明见解析。
成立.证明见解析。
【解析】试题分析:(1)取![]() 的中点
的中点![]() ,连结
,连结![]() ,证明四边形
,证明四边形![]() 是平行四边形,可得
是平行四边形,可得![]() ,利用线面平行的判定,即可得出结论;(2)由线面垂直得
,利用线面平行的判定,即可得出结论;(2)由线面垂直得![]() ,由矩形性质得
,由矩形性质得![]() ,由线面垂直的判定定理可得
,由线面垂直的判定定理可得![]() 平面
平面![]() ,由此能证明
,由此能证明![]() ;(3)当
;(3)当![]() 满足
满足![]() 时,能使
时,能使![]() 平面
平面![]() 成立,可利用等腰三角形的性质以及线面垂直的判定定理证明.
成立,可利用等腰三角形的性质以及线面垂直的判定定理证明.
试题解析:( ![]() )证明:取
)证明:取![]() 的中点
的中点![]() ,连接
,连接![]() ,
, ![]() .
.
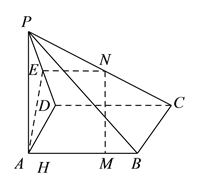
∵![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 中点,
中点,
∴![]() ,
,
又∵![]() ,
, ![]() 是
是![]() 中点,
中点,
∴![]() ,
,
∴![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() .
.
∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(![]() )∵
)∵![]() 平面
平面![]() ,
,
∴![]() ,
,
又![]() ,
,
∴![]() 平面
平面![]() ,
,
∴![]() ,
,
又∵![]()
∴![]() .
.
(![]() )当
)当![]() 满足
满足![]() 时,能使
时,能使![]() 平面
平面![]() 成立,
成立,
现证明如下:
∵![]() ,
, ![]() 是
是![]() 中点,
中点,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
由(![]() )可知
)可知![]() ,
,
∴![]() 平面
平面![]() .
.
故当![]() 满足
满足![]() 时,能使
时,能使![]() 平面
平面![]() 成立.
成立.
【方法点晴】本题主要考查线面平行的判定定理、直线和平面垂直的性质定理与判定定理,属于难题. 证明线面平行的常用方法:①利用线面平行的判定定理,使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线,可利用几何体的特征,合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行.②利用面面平行的性质,即两平面平行,在其中一平面内的直线平行于另一平面. 本题(1)是就是利用方法①证明的.


科目:高中数学 来源: 题型:
【题目】为了选拔优秀学生参加广州市高二级数学竞赛.现分别从他们在培训期间参加的若干次预赛成绩中随机抽取了5次,记录如下(单位:分):
甲 83 81 79 95 92
乙 92 85 75 88 90
(1)甲乙两人分数的极差分别是多少?并用茎叶图表示这两组数据.
(2)甲乙两人这5次成绩的平均分和方差各是多少?从稳定性的角度考虑,你认为选派哪位学生参加比赛较合适?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某居民区随机抽取10个家庭,获得第i个家庭的月收入xi(单位:千元)与月储蓄yi(单位:千元)的数据资料,算得 ![]() =80,
=80, ![]() =20,
=20, ![]() iyi=184,
iyi=184, ![]()
![]() =720.(b=
=720.(b= 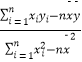 )
)
(1)求家庭的月储蓄y对月收入x的线性回归方程;
(2)判断变量x与y之间是正相关还是负相关;
(3)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知美国苹果公司生产某款iPhone手机的年固定成本为40万美元,每生产1万只还需另投入16万美元.设苹果公司一年内共生产该款iPhone手机x万只并全部销售完,每万只的销售收入为R(x)万美元,且R(x)=
(1)写出年利润W(万美元)关于年产量x(万只)的函数解析式;
(2)当年产量为多少万只时,苹果公司在该款iPhone手机的生产中所获得的利润最大?并求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数y=f(x)在R上可导且满足不等式xf′(x)+f(x)>0恒成立,且常数a,b满足a>b,则下列不等式一定成立的是( )
A.af(a)>bf(b)
B.af(b)>bf(a)
C.af(a)<bf(b)
D.af(b)<bf(a)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+bx+c,满足f(1)=﹣![]() , 且3a>2c>2b.
, 且3a>2c>2b.
(1)求证:a>0时,![]() 的取值范围;
的取值范围;
(2)证明函数f(x)在区间(0,2)内至少有一个零点;
(3)设x1 , x2是函数f(x)的两个零点,求|x1﹣x2|的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用二分法研究函数f(x)=x3+3x﹣1的零点时,第一次经计算f(0)<0,f(0.5)>0,可得其中一个零点x0∈ ,第二次应计算的f(x)的值为f( ).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com