
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:
| 1 | a2+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 3 |
| a |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年安徽省巢湖市无为中学高一(上)期中数学试卷(解析版) 题型:解答题
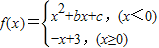 ,且f(-4)=f(0),f(-2)=-1.
,且f(-4)=f(0),f(-2)=-1.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年安徽省马鞍山市高三第一次教学质量检测理科数学试卷(解析版) 题型:解答题
(本题满分14分)设函数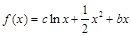
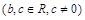 ,且
,且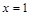 为
为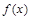 的极值点.
的极值点.
(Ⅰ) 若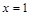 为
为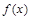 的极大值点,求
的极大值点,求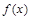 的单调区间(用
的单调区间(用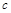 表示);
表示);
(Ⅱ) 若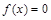 恰有两解,求实数
恰有两解,求实数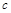 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:高考真题 题型:解答题
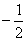 。
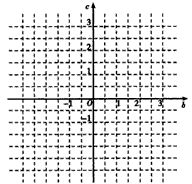
。 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com