
 .
.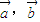 是否共线?请说明理由.
是否共线?请说明理由.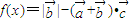 的最大值.
的最大值. 是否共线,只要根据向量共线的坐标表示代入检验即可
是否共线,只要根据向量共线的坐标表示代入检验即可 及
及 ,代入整理可得f(x)=-2sin2x+sinx,根据二次函数的性质及sinx∈(0,1]可求函数f(x)的最大值
,代入整理可得f(x)=-2sin2x+sinx,根据二次函数的性质及sinx∈(0,1]可求函数f(x)的最大值 共线.…(1分)
共线.…(1分) 共线.…(5分)
共线.…(5分) =
= =
= =
= =2|sinx|,…(7分)
=2|sinx|,…(7分) |=2sinx.…(8分)
|=2sinx.…(8分) =(cosx+sin2x,sinx+1-cos2x)
=(cosx+sin2x,sinx+1-cos2x) =(cosx+sin2x,sinx+1-cos2x)•(0,1)=sinx+1-cos2x=sinx+2sin2x…(10分)
=(cosx+sin2x,sinx+1-cos2x)•(0,1)=sinx+1-cos2x=sinx+2sin2x…(10分)
 时函数f(x)的最大值
时函数f(x)的最大值


科目:高中数学 来源: 题型:
| a |
| b |
| c |
| a |
| b |
| a |
| b |
| a |
| b |
| c |
| d |
| a |
| b |
| d |
| c |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| 3 |
| b |
| a |
| b |
| a |
| b |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| e1 |
| e2 |
| b |
| e1 |
| e2 |
| e1 |
| e2 |
| a |
| b |
| a |
| b |
| a |
| b |
查看答案和解析>>
科目:高中数学 来源:黄冈中学 高二数学(下册)、考试卷3 空间的角度与距离同步测试卷 题型:044
如图,已知向量![]() ,可构成空间向量的一组基底,若
,可构成空间向量的一组基底,若![]() ,
,![]() ,
,![]() ,在向量已有的运算法则基础上,新定义一种运算
,在向量已有的运算法则基础上,新定义一种运算![]() .显然a×b的结果仍为一向量,记作p.
.显然a×b的结果仍为一向量,记作p.

(1)求证:向量p为平面OAB的法向量;
(2)求证:以OA,OB为边的平行四边形OADB面积等于|a×b|;
(3)将得到四边形OADB按向量![]() 平移,得到一个平行六面体
平移,得到一个平行六面体![]() ,试判断平行六面体的体积V与|(a×b)·c|的大小.
,试判断平行六面体的体积V与|(a×b)·c|的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com