
(1)求证:当F、A、D不共线时,线段MN总平行于平面FAD;
(2)“不管怎样翻折矩形ABEF,线段MN总和线段FD平行.”这个结论对吗?如果对,请证明;如果不对,请说明能否改变个别已知条件使上述结论成立.

解析:(1)说明MN总平行于平面FAD的方法有两种,一是MN在一个总是与平面FAD平行的平面内;二是平面FAD内总有一条直线与MN平行.另外,对于折叠问题,要分析平面图形,搞清折叠前后量的变化.
(1)证明:在平面图形中,连结MN,设MN与AB交于点G.

由于ABCD和ABEF都是矩形且AD=AF,从而有AD∥BE且AD=BE,
∴四边形ADBE是平行四边形.
又AM=DN,根据比例关系得到MN∥AD.
折叠之后,MG∥AF,NG∥AD,如右图∴平面ADF∥平面GNM.
又MN![]() 平面GNM,∴MN∥平面ADF.
平面GNM,∴MN∥平面ADF.
∴当F、A、D不共线时,MN总平行于平面ADF.
(2)解:这个结论不对.要使上述结论成立,M、N应为AE和DB的中点,由于平面MNG∥平面FDA,可知要使MN∥FD总成立,根据面面平行的性质定理,只要FD与MN共面即可.
若要使FD与MN共面,连结FM,只要FM与DN相交即可.
由平面图形知,若要DN和FM共面,应有DN与FM相交于点B,折叠后的图应使F、M、B三点共线即可.


科目:高中数学 来源: 题型:
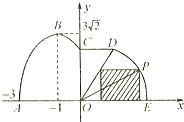 如图,某市拟在道路的一侧修建一条运动赛道,赛道的前一部分为曲线段ABC,该曲线段为函数y=Asin(ωx+φ)(A>0,ω>0,
如图,某市拟在道路的一侧修建一条运动赛道,赛道的前一部分为曲线段ABC,该曲线段为函数y=Asin(ωx+φ)(A>0,ω>0,| π |
| 2 |
| 2 |
| 3 |
 |
| DE |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,在△ABC中,AC=1,AB=3,∠ACB=
如图所示,在△ABC中,AC=1,AB=3,∠ACB=| π | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,在△ABC中,AC=1,AB=3,∠ACB=
如图所示,在△ABC中,AC=1,AB=3,∠ACB=| π | 2 |
查看答案和解析>>
科目:高中数学 来源:2011年江苏省南京市金陵中学高考数学预测试卷(2)(解析版) 题型:解答题
 <φ<π),x∈[-3,0]的图象,且图象的最高点为B(-1,3
<φ<π),x∈[-3,0]的图象,且图象的最高点为B(-1,3 );赛道的中间部分为
);赛道的中间部分为 千米的水平跑到CD;赛道的后一部分为以O圆心的一段圆弧
千米的水平跑到CD;赛道的后一部分为以O圆心的一段圆弧 .
.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省高三预测卷2数学 题型:解答题
(本小题满分14分)
如图,某市拟在道路的一侧修建一条运动赛道,赛道的前一部分为曲线段ABC,该曲线段为函数y= (A>0,
(A>0, >0,
>0, <
< <
< ),x∈[-3,0]的图象,且图象的最高点为B(-1,
),x∈[-3,0]的图象,且图象的最高点为B(-1, );赛道的中间部分为
);赛道的中间部分为 千米的水平跑到CD;赛道的后一部分为以O圆心的一段圆弧
千米的水平跑到CD;赛道的后一部分为以O圆心的一段圆弧 .
.

(1)求 ,
, 的值和∠DOE的值;
的值和∠DOE的值;
(2)若要在圆弧赛道所对应的扇形区域内建一个“矩形草坪”,如图所示,矩形的一边在道路AE上,一个顶点在扇形半径OD上.记∠POE= ,求当“矩形草坪”的面积最大时
,求当“矩形草坪”的面积最大时 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com