
【题目】甲乙两种商品在过去一段时间内的价格走势如图所示,假设某人持有资金120万元,他可以在t1至t4的任意时刻买卖这两种商品,且买卖能够立即成交(其他费用忽略不计),那么他持有的资金最多可变为( ) 
A.120万元
B.160万元
C.220万元
D.240万元
 天天向上口算本系列答案
天天向上口算本系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知圆C1:(x+1)2+y2=1,圆C2:(x﹣3)2+(y﹣4)2=1.
(Ⅰ)若过点C1(﹣1,0)的直线l被圆C2截得的弦长为 ![]() ,求直线l的方程;
,求直线l的方程;
(Ⅱ)圆D是以1为半径,圆心在圆C3:(x+1)2+y2=9上移动的动圆,若圆D上任意一点P分别作圆C1的两条切线PE,PF,切点为E,F,求 ![]() 的取值范围;
的取值范围;
(Ⅲ)若动圆C同时平分圆C1的周长、圆C2的周长,则动圆C是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种平面分形如图所示,一级分形图是由一点出发的三条线段,长度均为1,两两 夹角为120°; 二级分形图是在一级分形图的每条线段的末端出发再生成两条长度为原来 ![]() 的线段,且这两条线段与原线段两两夹角为120°;…;依此规律得到n级分形图,则n级分形图中所有线段的长度之和为. .
的线段,且这两条线段与原线段两两夹角为120°;…;依此规律得到n级分形图,则n级分形图中所有线段的长度之和为. . 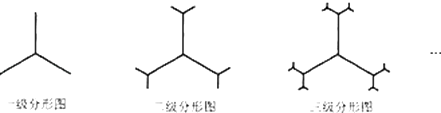
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,已知∠ABC=45°,O在AB上,且OB=OC= ![]() AB,又PO⊥平面ABC,DA∥PO,DA=AO=
AB,又PO⊥平面ABC,DA∥PO,DA=AO= ![]() PO.
PO. 
(Ⅰ)求证:PD⊥平面COD;
(Ⅱ)求二面角B﹣DC﹣O的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】求满足下列条件的直线方程:
(1)求经过直线l1:x+3y﹣3=0和l2:x﹣y+1=0的交点,且平行于直线2x+y﹣3=0的直线l的方程;
(2)已知直线l1:2x+y﹣6=0和点A(1,﹣1),过点A作直线l与l1相交于点B,且|AB|=5,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD﹣A1B1C1D1的棱长为1,N为CD1中点,M为线段BC1上的动点,(M不与B,C1重合)有四个命题:
①CD1⊥平面BMN;
②MN∥平面AB1D1;
③平面AA1CC1⊥平面BMN;
④三棱锥D﹣MNC的体积有最大值.
其中真命题的序号是 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x .
(1)解方程f(log4x)=3;
(2)已知不等式f(x+1)≤f[(2x+a)2](a>0)对x∈[0,15]恒成立,求实数a的取值范围;
(3)存在x∈(﹣∞,0],使|af(x)﹣f(2x)|>1成立,试求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com