②③
分析:①利用三角函数的平移变换即可判断出;
②利用导数的几何意义、导数研究函数的单调性即可判断出;
③利用正方体的内切球、外接球的半径与正方体的半径之间的关系即可得出;
④利用斜率存在的两条直线平行的充要条件即可得出.
解答:①把函数y=3sin(2x+

)的图象向右平移

个单位得到y=3
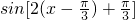
=
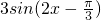
的图象,而得不到函数y=3sin2x的图象,因此不正确;
②∵函数f(x)=ax
2-lnx的图象在x=1处的切线平行于直线y=x,∴
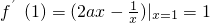
,解得a=1,
∴
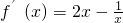
=
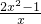
,(x>0),令f
′(x)=0,解得x=

,当

时,f
′(x)>0,∴(
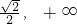
)是f(x)的单调递增区间,因此正确;
③不妨设此正方体的棱长为2,则其内切球与外接球的半径分别为1,

,故其内切球与其外接球的表面积之比=
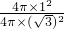
=

,因此正确;
④∵“a=2”?“直线ax+2y=0平行于直线x+y=1”,∴“a=2”是“直线ax+2y=0平行于直线x+y=1”的充分必要条件.故④不正确.
综上可知:只有②③正确.
故答案为②③.
点评:本题综合考查了三角函数的平移变换、导数的几何意义和利用导数研究函数的单调性、正方体的内切球、外接球的半径与正方体的半径之间的关系及斜率存在的两条直线平行的充要条件,熟练以上知识与方法是解题的关键.

 )的图象向右平移
)的图象向右平移 个单位,得到y=3sin2x的图象;
个单位,得到y=3sin2x的图象;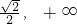 )是f(x)的单调递增区间;
)是f(x)的单调递增区间; )的图象向右平移
)的图象向右平移 个单位得到y=3
个单位得到y=3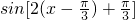 =
=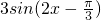 的图象,而得不到函数y=3sin2x的图象,因此不正确;
的图象,而得不到函数y=3sin2x的图象,因此不正确;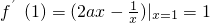 ,解得a=1,
,解得a=1,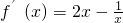 =
=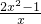 ,(x>0),令f′(x)=0,解得x=
,(x>0),令f′(x)=0,解得x= ,当
,当 时,f′(x)>0,∴(
时,f′(x)>0,∴(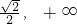 )是f(x)的单调递增区间,因此正确;
)是f(x)的单调递增区间,因此正确; ,故其内切球与其外接球的表面积之比=
,故其内切球与其外接球的表面积之比=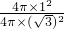 =
= ,因此正确;
,因此正确;

 初中学业考试导与练系列答案
初中学业考试导与练系列答案 的图象向右平移
的图象向右平移 个单位,得到
个单位,得到 的图象;
的图象; 的图象在x=1处的切线平行于直线y=x,则
的图象在x=1处的切线平行于直线y=x,则 是f(x)的单调递增区间;
是f(x)的单调递增区间;