
在△ABC中, 分别为角
分别为角 所对的三边,已知
所对的三边,已知
(Ⅰ)求 的值
的值
(Ⅱ)若 ,求边
,求边 的长.
的长.
(Ⅰ)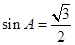 ;(Ⅱ)
;(Ⅱ)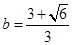 .
.
解析试题分析:(Ⅰ)求 的值,可考虑利用正弦定理,也可利用面积公式
的值,可考虑利用正弦定理,也可利用面积公式 ,但本题已知
,但本题已知 ,显然是余弦定理形式,可考虑利用余弦定理求出
,显然是余弦定理形式,可考虑利用余弦定理求出 ,因此对
,因此对 变形为
变形为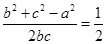 ,可得
,可得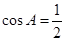 ,从而求出
,从而求出 的值;(Ⅱ)若
的值;(Ⅱ)若 ,求边
,求边 的长,可利用余弦定理,也可利用正弦定理来求,本题由(Ⅰ)知
的长,可利用余弦定理,也可利用正弦定理来求,本题由(Ⅰ)知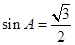 ,只要能求出
,只要能求出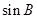 ,利用余弦定理即可解决,由已知
,利用余弦定理即可解决,由已知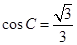 ,利用
,利用 ,根据两角和与差的正弦公式即可求出,从而求出边
,根据两角和与差的正弦公式即可求出,从而求出边 的长.
的长.
试题解析:(Ⅰ)∵b2+c2-a2=bc,cosA=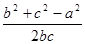 =
=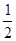 (3分)
(3分)
又∵ ∴sinA=
∴sinA=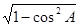 =
=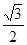 (5分)
(5分)
(Ⅱ)在△ABC中,sinA=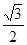 ,a=
,a=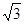 ,cosC=
,cosC=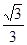
可得sinC=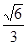 (6分)
(6分)
∵A+B+C=p
∴sinB ="sin(A+C)=" 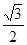 ×
×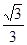 +
+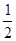 ×
×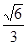 =
= (9分)
(9分)
由正弦定理知: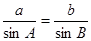
∴b= =
= =
=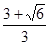 . (12分)
. (12分)
考点:解三角形.


科目:高中数学 来源: 题型:解答题
辽宁广播电视塔位于沈阳市沈河区青年公园西侧,蜿蜒的南运河带状公园内,占地8000平方米.全塔分为塔座、塔身、塔楼和桅杆四部分.某数学活动小组在青年公园内的A处测得塔顶B处的仰角为45°. 在水平地面上,沿着A点与塔底中心C处连成的直线行走129米后到达D处(假设可以到达),此时测得塔顶B处的仰角为60°.
(1)请你根据题意,画出一个ABCD四点间的简单关系图形;
(2)根据测量结果,计算辽宁广播电视塔的高度(精确到1米).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com