
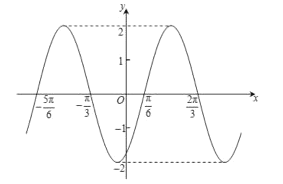
【题目】函数![]() 的图象如图所示,为了得到函数
的图象如图所示,为了得到函数![]() 的图象,可以把函数
的图象,可以把函数![]() 的图象( )
的图象( )
A.先向左平移![]() 个单位,再把所得各点的横坐标伸长到原来的
个单位,再把所得各点的横坐标伸长到原来的![]() 倍(纵坐标不变)
倍(纵坐标不变)
B.先向左平移![]() 个单位,再把所得各点的横坐标缩短到原来的
个单位,再把所得各点的横坐标缩短到原来的![]() (纵坐标不变)
(纵坐标不变)
C.每个点的横坐标缩短到原来的![]() (纵坐标不变),再向左平移
(纵坐标不变),再向左平移![]() 个单位
个单位
D.每个点的横坐标伸长到原来的![]() 倍(纵坐标不变),再向左平移
倍(纵坐标不变),再向左平移![]() 个单位
个单位
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),圆
为参数),圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 的方程和圆
的方程和圆![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() 为圆
为圆![]() 上一动点,求点
上一动点,求点![]() 到直线
到直线![]() 的最小距离.
的最小距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
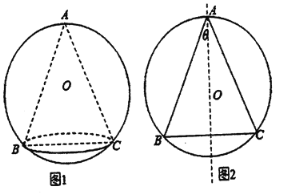
【题目】某艺术品公司欲生产一款迎新春工艺礼品,该礼品是由玻璃球面和该球的内接圆锥组成,圆锥的侧面用于艺术装饰,如图1.为了便于设计,可将该礼品看成是由圆O及其内接等腰三角形![]() 绕底边
绕底边![]() 上的高所在直线
上的高所在直线![]() 旋转
旋转![]() 而成,如图2.已知圆O的半径为
而成,如图2.已知圆O的半径为![]() ,设
,设![]() ,
,![]() ,圆锥的侧面积为
,圆锥的侧面积为![]() (S圆锥的侧面积
(S圆锥的侧面积![]() (R-底面圆半径,I-母线长))
(R-底面圆半径,I-母线长))
(1)求S关于![]() 的函数关系式;
的函数关系式;
(2)为了达到最佳观赏效果,要求圆锥的侧面积S最大.求S取得最大值时腰![]() 的长度
的长度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某地区观众对大型综艺活动《中国好声音》的收视情况,随机抽取了100名观众进行调查,其中女性有55名.下面是根据调查结果绘制的观众收看该节目的场数与所对应的人数表:
场数 | 9 | 10 | 11 | 12 | 13 | 14 |
人数 | 10 | 18 | 22 | 25 | 20 | 5 |
将收看该节目场次不低于13场的观众称为“歌迷”,已知“歌迷”中有10名女性.
(1)根据已知条件完成下面的2×2列联表,并据此资料我们能否有95%的把握认为“歌迷”与性别有关?
非歌迷 | 歌迷 | 合计 | |
男 | |||
女 | |||
合计 |
(2)将收看该节目所有场次(14场)的观众称为“超级歌迷”,已知“超级歌迷”中有2名女性,若从“超级歌迷”中任意选取2人,求至少有1名女性观众的概率.
P(K2≥k) | 0.05 | 0.01 |
k | 3.841 | 6.635 |
附:K2=![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a为常数,函数f(x)=x(lnx﹣1)﹣ax2,给出以下结论:(1)f(x)存在唯一零点与a的取值无关;(2)若a=e﹣2,则f(x)存在唯一零点;(3)若a<e﹣2,则f(x)存在两个零点.其中正确的个数是( )
A.3B.2C.1D.0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com