
分析 g(x)=ln|x|的图象经过点(1,0),数形结合可得 f(1)=$\frac{1}{2}$•12+m<0,由此解得m的值.
解答 解:∵函数f(x)=$\frac{1}{2}$x2+m的图象(图中黑色部分)与函数g(x)=ln|x|的图象(图中红色部分)有四个交点,
再根据这两个函数都是偶函数,它们的图象关于y轴对称,故它们的图象在(0,+∞)上有两个交点.
又g(x)=ln|x|的图象经过点(1,0),数形结合可得 f(1)=$\frac{1}{2}$•12+m<0,解得m<$\frac{1}{2}$,
故答案为:(-∞,$\frac{1}{2}$).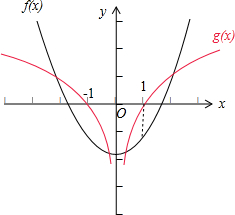
点评 本题考查了根的存在性及根的个数判断,以及函数与方程的思想,属于中档题.


科目:高中数学 来源: 题型:解答题
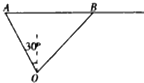 某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口O北偏西30°且与该港口相距20海里的A处,并正以30海里/小时的航行速度沿正东方向匀速行驶,经过t小时与轮船相遇.
某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口O北偏西30°且与该港口相距20海里的A处,并正以30海里/小时的航行速度沿正东方向匀速行驶,经过t小时与轮船相遇.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com