
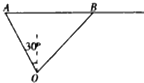
 ij�ۿ�OҪ��һ����Ҫ��Ʒ��Сͧ�͵�һ�����ں��е��ִ��ϣ���Сͧ����ʱ���ִ�λ�ڸۿ�O��ƫ��30������øۿ����20�����A����������30����/Сʱ�ĺ����ٶ�����������������ʻ������tСʱ���ִ�������
ij�ۿ�OҪ��һ����Ҫ��Ʒ��Сͧ�͵�һ�����ں��е��ִ��ϣ���Сͧ����ʱ���ִ�λ�ڸۿ�O��ƫ��30������øۿ����20�����A����������30����/Сʱ�ĺ����ٶ�����������������ʻ������tСʱ���ִ����������� ��I����OC��AB����OCΪСͧ����̺���·�̣�����ִ��ĺ���ʱ���OC�ľ��뼴�ɵó�Сͧ�ĺ����ٶȣ�
��II����Сͧ���ִ���B���������������Ҷ������㺽��ʱ��t���ó�AB��OB���룬�Ӷ��ó���COB�Ķ������ó����з�����
��� 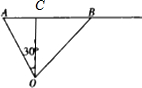 �⣺��I����O��OC��AB������ΪC����OC=OAcos30��=10$\sqrt{3}$��
�⣺��I����O��OC��AB������ΪC����OC=OAcos30��=10$\sqrt{3}$��
�ʵ�Сͧ���о������ʱ��·��Ϊ10$\sqrt{3}$��
�ִ�����·��ΪAC=$\frac{1}{2}$OA=10��
�ຽ��ʱ��Ϊt=$\frac{10}{30}$=$\frac{1}{3}$��
��Сͧ�ĺ����ٶ�Ϊ$\frac{10\sqrt{3}}{\frac{1}{3}}$=30$\sqrt{3}$����/ʱ��
��II����Сͧ���ִ���B��������
�ڡ�AOB�У���OAB=60�㣬OB=30t��AB=30t��OA=20��
�����Ҷ����ã�OB2=AB2+OA2-2��AB��OAcos��OAB
����30t��2=400+900t2-1200tcos60��
��600t=400
��ã�t=$\frac{2}{3}$����AB=OB=20��
���OABΪ�ȱ������Σ����BOC=30�㣮
�ʺ��з���Ϊ��ƫ��30�㣬�����ٶ�Ϊ30����/Сʱ��Сͧ�������ʱ�����ִ�������
���� ���⿼���˽������ε�Ӧ�ã����Ҷ����������е��⣮


 �Ƹ������������ϵ�д�
�Ƹ������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
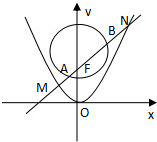 ��֪��F��������C��x2=2py��p��0���Ľ��㣬��P��3��y0����y0��1����������C��һ�㣬��$|{PF}|=\frac{13}{4}$����Q�ķ���Ϊx2+��y-3��2=6������F��ֱ��l����������C�͡�Q���ν���M��A��B��N������ͼ��ʾ��
��֪��F��������C��x2=2py��p��0���Ľ��㣬��P��3��y0����y0��1����������C��һ�㣬��$|{PF}|=\frac{13}{4}$����Q�ķ���Ϊx2+��y-3��2=6������F��ֱ��l����������C�͡�Q���ν���M��A��B��N������ͼ��ʾ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
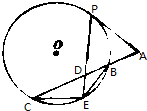 ��ͼ����֪PA��ԲO���У�PΪ�е㣬����ABC��ԲO�����ڵ�B��C��AC=2PA��DΪAC���е㣮PD���ӳ��߽�ԲO��E�㣬֤����
��ͼ����֪PA��ԲO���У�PΪ�е㣬����ABC��ԲO�����ڵ�B��C��AC=2PA��DΪAC���е㣮PD���ӳ��߽�ԲO��E�㣬֤�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 8 | B�� | 10 | C�� | 12 | D�� | 14 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com