
分析 (1)不等式等价于2x<(x+2)ln(1+x),令g(x)=2x-(x+2)ln(1+x),求出导数和二阶导数,判断g(x)的单调性得出g(x)<g(0)=0;
(2)不等式等价于$\frac{(x+1)ln(x+1)-x-k{x}^{2}}{x}$<0,令g(x)=(1+x)ln(1+x)-x-kx2,求出导数和二阶导数判断g(x)的单调性,得出g(x)的符号从而得出k的值.
解答 证明:(1)f(x)<$\frac{1}{2}$x+1?$\frac{x}{ln(1+x)}$<$\frac{x+2}{2}$?2x<(x+2)ln(1+x)(x>0),
令g(x)=2x-(x+2)ln(1+x),
则g′(x)=2-ln(x+1)-$\frac{x}{x+1}$-$\frac{2}{x+1}$=$\frac{x-(x+1)ln(x+1)}{x+1}$,
令x+1=t,则g′(x)=$\frac{t-tlnt-1}{t}$(t>1).
令h(t)=t-tlnt-1,则h′(t)=1-lnt-1-1=-1-lnt<0.
∴h(t)在(1,+∞)上是减函数,∴h(t)<h(1)=0,
∴g′(x)<0,∴g(x)在(0,+∞)上是减函数,
∴g(x)<g(0)=0,
∴2x<(x+2)ln(x+1),
∴f(x)<$\frac{1}{2}$x+1.
解:(2)∵f(x)=$\frac{x}{ln(x+1)}$>0,
∴(1+kx)f(x)>1+x?1+kx>$\frac{x+1}{f(x)}$=$\frac{(x+1)ln(x+1)}{x}$?$\frac{(x+1)ln(x+1)-x-k{x}^{2}}{x}$<0,
令g(x)=(1+x)ln(1+x)-x-kx2,
则g′(x)=ln(1+x)-2kx,
g″(x)=$\frac{1}{1+x}-2k$,
①x>0时,有0<$\frac{1}{1+x}$<1,
令2k≥1,则g″(x)<0,
故g′(x)在(0,+∞)上是减函数,∴g′(x)<g′(0)=0,
∴g(x)在(0,+∞)上是减函数,
从而,g(x)<g(0)=0,
∴k≥$\frac{1}{2}$时,对于x>0,有$\frac{(x+1)ln(x+1)-x-k{x}^{2}}{x}$<0,
②-1<x<0时,有$\frac{1}{x+1}$>1,
令2k≤1,则g″(x)>0,
故g′(x)在(-1,0)上是增函数,∴g′(x)<g′(0)=0
∴g(x)在(-1,0)上是减函数.
从而,g(x)>g(0)=0.
∴当k≤$\frac{1}{2}$时,对于-1<x<0,有$\frac{(x+1)ln(x+1)-x-k{x}^{2}}{x}$<0.
综上,k=$\frac{1}{2}$.
点评 本题考察了函数的单调性,导数的应用,不等式的证明,本题是一道中档题.


科目:高中数学 来源: 题型:解答题
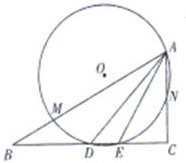 如图,已知在△ABC中,AE,AD分别为其角平分线和中线,△ADE的外接圆为⊙O,⊙O与AB,AC分别交于M,N,求证:
如图,已知在△ABC中,AE,AD分别为其角平分线和中线,△ADE的外接圆为⊙O,⊙O与AB,AC分别交于M,N,求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数F(x)=$\frac{f(x)}{x}$在(0,+∞)上为增函数 | B. | 函数F (x)=$\frac{f(x)}{x}$在(0,+∞)上为减函数 | ||
| C. | 函数G(x)=xf(x)在(0,+∞)上为增函数 | D. | 函数G(x)=xf(x)在(0,+∞)上为减函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
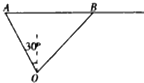 某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口O北偏西30°且与该港口相距20海里的A处,并正以30海里/小时的航行速度沿正东方向匀速行驶,经过t小时与轮船相遇.
某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口O北偏西30°且与该港口相距20海里的A处,并正以30海里/小时的航行速度沿正东方向匀速行驶,经过t小时与轮船相遇.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -20 | B. | -15 | C. | 15 | D. | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $6\sqrt{2}$ | C. | 12 | D. | $8\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com