
分析 (I)通过对f(x)=aex(a为正实数)求导,判断函数f(x)=aex(a为正实数)在区间[0,+∞)上的单调性,进而整理即得结论;
(Ⅱ)通过分析问题转化为证明ex-x-1>0,令g(x)=ex-x-1,问题即为证明g(x)的最小值为0,通过导数、结合单调性即得结论.
解答 (I)解:∵f(x)=aex(a为正实数),ex>0,
∴f′(x)=aex>0(a为正实数),即函数f(x)=aex(a为正实数)在R上单调递增,
∴函数f(x)在区间[0,+∞)上的最小值为f(0)=a;
(Ⅱ)证明:当a=1时,f(x)=ex,
要证f(x)≥x+1,即证ex-x-1>0,
令g(x)=ex-x-1,则g′(x)=ex-1,
令g′(x)=ex-1=0可知x=0,
故当x<0时,g′(x)=ex-1<1-1=0,即g(x)=ex-x-1在(-∞,0)上单调递减,
当x>0时,g′(x)=ex-1>1-1=0,即g(x)=ex-x-1在(-∞,0)上单调递增,
从而当x=0时,g(x)取得最小值g(0)=1-0-1=0,
∴ex-x-1>0,即f(x)≥x+1.
点评 本题考查利用导数研究函数的单调性及证明不等式问题,考查转化思想,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $y=-\frac{1}{x}$ | B. | y=3-x-3x | C. | $y=ln({x+\sqrt{1+{x^2}}})$ | D. | $y=\frac{{{3^x}+1}}{{{3^x}-1}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
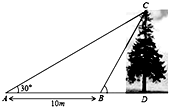 如图,某数学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上).请你根据他们测量数据计算这棵树CD的高度5$\sqrt{3}$m.
如图,某数学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上).请你根据他们测量数据计算这棵树CD的高度5$\sqrt{3}$m.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
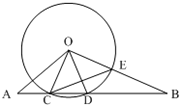 如图,⊙O的半径为 4,线段AB与⊙O相交于点C、D,AC=2,∠BOD=∠A,OB与⊙O相交于点E.
如图,⊙O的半径为 4,线段AB与⊙O相交于点C、D,AC=2,∠BOD=∠A,OB与⊙O相交于点E.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1-2i | B. | -1+2i | C. | 1+2i | D. | 1-2i |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com