
| A. | $y=-\frac{1}{x}$ | B. | y=3-x-3x | C. | $y=ln({x+\sqrt{1+{x^2}}})$ | D. | $y=\frac{{{3^x}+1}}{{{3^x}-1}}$ |
分析 利用基本初等函数的性质对选项逐项判断即可.
解答 解:对于A:反比例函数,图象在二、四象限,是奇函数,但在整个定义域内不连续,没有单调性,故A不对.
对于B:令t=3x,y=$\frac{1}{t}-t$,是奇函数,但在其定义域内是减函数,故B不对.
对于C:f(x)+f(-x)=$ln(x+\sqrt{1+{x}^{2}})+ln(-x+\sqrt{1+{x}^{2}})$=0,是奇函数,根据复合函数的单调性,同增异减,所以在其定义域内是增函数,故C对.
对于D:$y=\frac{{3}^{x}+1}{{3}^{x}-1}=1+\frac{2}{{3}^{x}-1}$,在其定义域内是减函数,故D不对.
故选C.
点评 本题考查函数的单调性,需要熟练应用常用函数的性质和图象,属于基础题.


科目:高中数学 来源: 题型:解答题
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 张梦雪 | 10.2 | 10.3 | 9.8 | 10.1 | 10 | 9.3 | 10.9 | 9.9 | 10.3 | 9.2 |
| 巴特萨拉斯基纳 | 10.1 | 10 | 10.4 | 10.2 | 9.2 | 9.2 | 10.5 | 10.2 | 9.5 | 9.7 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
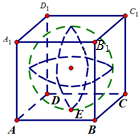 已知棱长为1的正方体有一个内切球(如图),E为ABCD的中心,A1E与球相交于FE,则EF的长为$\frac{{\sqrt{6}}}{3}$.
已知棱长为1的正方体有一个内切球(如图),E为ABCD的中心,A1E与球相交于FE,则EF的长为$\frac{{\sqrt{6}}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
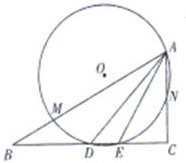 如图,已知在△ABC中,AE,AD分别为其角平分线和中线,△ADE的外接圆为⊙O,⊙O与AB,AC分别交于M,N,求证:
如图,已知在△ABC中,AE,AD分别为其角平分线和中线,△ADE的外接圆为⊙O,⊙O与AB,AC分别交于M,N,求证:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com