
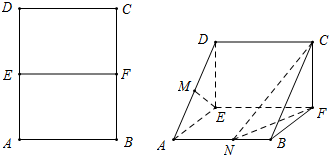
分析 (I)由EF⊥平面ADE得出EF⊥平面ADE得出AB⊥平面ADE,故而AB⊥EM,结合EM⊥AD得出EM⊥平面ABCD,故结论成立;
(II)由CN为三棱锥C-BFN的外接球的直径得出BN,从而计算棱锥的体积.
解答 证明:(Ⅰ)∵EF是矩形ABCD的中位线,
∴EF⊥AE,EF⊥DE,
∴EF⊥平面AED.又AB∥EF,
∴AB⊥平面AED,又EM?平面AED,
∴EM⊥AB,
又在等腰△AED中,M是AD中点,
∴EM⊥AD,
∴EM⊥平面ABCD,又CN?平面ABCD,
∴EM⊥CN.
解:(Ⅱ)设三棱锥C-BFN的外接球半径为r,则$\frac{4}{3}π{r}^{3}$=$\frac{8\sqrt{2}}{3}π$,
解得r=$\sqrt{2}$.∴CN=2r=2$\sqrt{2}$.
∴BN2+BF2+CF2=CN2=8,
∴BN=2,
VC-BFN=$\frac{1}{3}{S}_{△BFN}$•CF=$\frac{1}{3}$×$\frac{1}{2}×\sqrt{2}×2×\sqrt{2}$=$\frac{2}{3}$.
点评 本题考查了线面垂直的判定,棱锥与外接球的位置关系,棱锥的体积计算,属于中档题.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案科目:高中数学 来源: 题型:选择题
| A. | $y=-\frac{1}{x}$ | B. | y=3-x-3x | C. | $y=ln({x+\sqrt{1+{x^2}}})$ | D. | $y=\frac{{{3^x}+1}}{{{3^x}-1}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
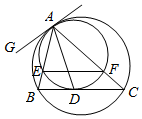 如图,已知半径不等的两圆均与直线AG相切于点A,大圆的弦BC与小圆相切于点D,
如图,已知半径不等的两圆均与直线AG相切于点A,大圆的弦BC与小圆相切于点D,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
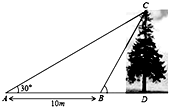 如图,某数学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上).请你根据他们测量数据计算这棵树CD的高度5$\sqrt{3}$m.
如图,某数学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上).请你根据他们测量数据计算这棵树CD的高度5$\sqrt{3}$m.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
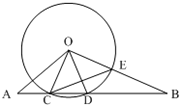 如图,⊙O的半径为 4,线段AB与⊙O相交于点C、D,AC=2,∠BOD=∠A,OB与⊙O相交于点E.
如图,⊙O的半径为 4,线段AB与⊙O相交于点C、D,AC=2,∠BOD=∠A,OB与⊙O相交于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com