
分析 (1)求出函数的导数,问题转化为$-2a≤\frac{1}{x}+2x$对x∈(0,+∞)都成立,根据函数的单调性求出a的范围即可;
(2)求出g(x)的导数,问题转化为方程$1+\frac{1}{x}-lnx=0$在[t,+∞)(t∈N*)上有解,令$φ(x)=1+\frac{1}{x}-lnx$(x>0),根据函数的单调性求出t的最大值即可.
解答 解:(1)函数f(x)的定义域为(0,+∞),
∵f(x)=lnx+x2+2ax,∴$f'(x)=\frac{1}{x}+2x+2a$.
∵函数f(x)在(0,+∞)上单调递增,
∴f'(x)≥0,即$\frac{1}{x}+2x+2a≥0$对x∈(0,+∞)都成立.…(2分)
∴$-2a≤\frac{1}{x}+2x$对x∈(0,+∞)都成立.
当x>0时,$\frac{1}{x}+2x≥2\sqrt{\frac{1}{x}•2x}=2\sqrt{2}$,当且仅当$\frac{1}{x}=2x$,即$x=\frac{{\sqrt{2}}}{2}$时,取等号.
∴$-2a≤2\sqrt{2}$,即$a≥-\sqrt{2}$.∴a的取值范围为$[{-\sqrt{2},+∞})$.…(5分)
(2)当$a=\frac{1}{2}$时,$g(x)=\frac{f(x)}{x+1}-x=\frac{{lnx+{x^2}+x}}{x+1}-x=\frac{lnx}{x+1}$.$g'(x)=\frac{{1+\frac{1}{x}-lnx}}{{{{({x+1})}^2}}}$.…(6分)
∵函数g(x)在[t,+∞)(t∈N*)上存在极值,
∴方程g'(x)=0在[t,+∞)(t∈N*)上有解,
即方程$1+\frac{1}{x}-lnx=0$在[t,+∞)(t∈N*)上有解.…(8分)
令$φ(x)=1+\frac{1}{x}-lnx$(x>0),
由于x>0,则$φ'(x)=-\frac{1}{x^2}-\frac{1}{x}<0$,∴函数φ(x)在(0,+∞)上单调递减.
∵$φ(3)=\frac{4}{3}-ln3=\frac{1}{3}ln$$\frac{e^4}{27}$$>\frac{1}{3}ln\frac{{{{2.5}^4}}}{27}>0$,$φ(4)=\frac{5}{4}-ln4=\frac{1}{4}ln$$\frac{e^5}{256}$$<\frac{1}{4}ln\frac{3^5}{256}<0$,
∴函数φ(x)的零点x0∈(3,4).
∵方程φ(x)=0在[t,+∞)(t∈N*)上有解,t∈N*∴t≤3.
∵t∈N*,∴t的最大值为3.…(12分)
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及转化思想,函数恒成立问题,是一道中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 若S9>S8,S9>S10,则S17>0,S18<0 | B. | 若S17>0,S18<0,则S9>S8,S8>S10 | ||
| C. | 若S17>0,S18<0,则a17>0,a18<0 | D. | 若a17>0,a18<0,则S17>0,S18<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 34 | B. | 27 | C. | -43 | D. | -6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
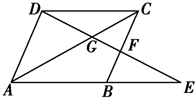 如图所示,在平行四边形ABCD中,点E是AB延长线上一点,DE交AC于点G,交BC于点F.
如图所示,在平行四边形ABCD中,点E是AB延长线上一点,DE交AC于点G,交BC于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com