
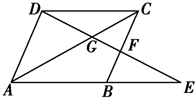
 如图所示,在平行四边形ABCD中,点E是AB延长线上一点,DE交AC于点G,交BC于点F.
如图所示,在平行四边形ABCD中,点E是AB延长线上一点,DE交AC于点G,交BC于点F.分析 (1)根据平行四边形两条对边平行,得到两对相似三角形.写出对应边成比例,得到两个比例式中各有两条线段的比相等,根据等量代换得到比例式,转化成乘积式,得到结论.
(2)做法同一类似,根据两条线段平行,根据平行得到对应线段成比例,在两个比例式中出现有一个比例相等,利用等量代换,得到结论.
解答 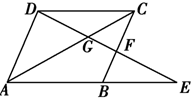 证明(1):∵BF∥AD,∴$\frac{AB}{AE}$=$\frac{DF}{DE}$.
证明(1):∵BF∥AD,∴$\frac{AB}{AE}$=$\frac{DF}{DE}$.
又∵CD∥BE,∴$\frac{CF}{CB}$=$\frac{DF}{DE}$,
∴$\frac{CF}{CB}$=$\frac{AB}{AE}$.
(2)∵CD∥AE,∴$\frac{DG}{GE}$=$\frac{CG}{AG}$.
又∵AD∥CF,∴$\frac{GF}{DG}$=$\frac{CG}{AG}$,
∴$\frac{DG}{GE}$=$\frac{GF}{DG}$,
即DG2=GE•GF.
点评 本题考查平行线分线段成比例定理,在题目中连续使用成比例定理,有两次使用等量代换,是一个比较典型的题目,实际上证明线段成比例是学习中的难点.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | n(n+1) | B. | n(n-1) | C. | $\frac{n(n+1)}{2}$ | D. | $\frac{n(n-1)}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
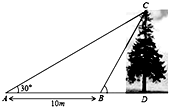 如图,某数学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上).请你根据他们测量数据计算这棵树CD的高度5$\sqrt{3}$m.
如图,某数学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上).请你根据他们测量数据计算这棵树CD的高度5$\sqrt{3}$m.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
喜欢户外运动情况 性别 | 喜欢户外运动 | 不喜欢户外运动 | 合计 |
| 男性 | 20 | ||
| 女性 | 15 | ||
| 合计 | 50 |
| P(x2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({\frac{1}{3},\frac{3}{4}})$ | B. | $({\frac{2}{3},\frac{3}{4}})$ | C. | (3,4) | D. | (4,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com