
分析 (1)注意到∠OPC=90°,动点P在以M($\frac{1}{2}$,0)为圆心,OC为直径的圆上,故可以求出圆心与半径,写出圆的标准方程;
(2)设动点M的坐标为(x,y),根据动点M到点F(1,0)的距离比它到y轴的距离大1,建立方程,化简可得点M的轨迹C的方程.
解答 解:(1)∵∠OPC=90°,动点P在以M($\frac{1}{2}$,0)为圆心,OC为直径的圆上,
∴所求点的轨迹方程为:(x-$\frac{1}{2}$)2+y2=1(0<x≤1);
(2)设动点M的坐标为(x,y),
由题意,∵动点M到点F(1,0)的距离比它到y轴的距离大1,
∴$\sqrt{(x-1)^{2}+{y}^{2}}$=|x|+1;
化简得y2=4x(x≥0)或y=0(x≤0),
∴点M的轨迹C的方程为y=4x(x≥0)或y=0(x<0).
点评 本题考查轨迹方程,考查了学生数形结合的思想和分析推理能力,是中档题.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若S9>S8,S9>S10,则S17>0,S18<0 | B. | 若S17>0,S18<0,则S9>S8,S8>S10 | ||
| C. | 若S17>0,S18<0,则a17>0,a18<0 | D. | 若a17>0,a18<0,则S17>0,S18<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “若a>1,则a2>1”的否命题是“若a>1,则a2≤1” | |
| B. | {an}为等比数列,则“a1<a2<a3”是“a4<a5”的既不充分也不必要条件 | |
| C. | ?x0∈(-∞,0),使${3^{x_0}}<{4^{x_0}}$成立 | |
| D. | “$tanα≠\sqrt{3}$”必要不充分条件是“$a≠\frac{π}{3}$” |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
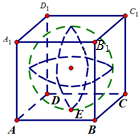 已知棱长为1的正方体有一个内切球(如图),E为ABCD的中心,A1E与球相交于FE,则EF的长为$\frac{{\sqrt{6}}}{3}$.
已知棱长为1的正方体有一个内切球(如图),E为ABCD的中心,A1E与球相交于FE,则EF的长为$\frac{{\sqrt{6}}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
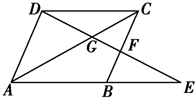 如图所示,在平行四边形ABCD中,点E是AB延长线上一点,DE交AC于点G,交BC于点F.
如图所示,在平行四边形ABCD中,点E是AB延长线上一点,DE交AC于点G,交BC于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com