
分析 (1)求导数,分类讨论,利用导数的正负,讨论f(x)的单调性;
(2)如果当x>1时,f(x)<-2a-1,(1,x)在f(x)递减区间,故$\frac{1}{a}$≤1<x,即可求实数a的取值范围;
(3)g(x)在区间[1,4]上不单调,g(x)在[1,4]上有极值,利用导数可求.
解答 解:(1)f'(x)=$\frac{(1+2x)(1-ax)}{{x}^{2}}$.令f'(x)=0,解得x1=-$\frac{1}{2}$,x2=$\frac{1}{a}$.
由题,显然x∈(0,﹢∞),故
①a=0时,f'(x)=$\frac{1+2x}{{x}^{2}}$>0,则f(x)单调递增;
②a<0时,f'(x)>0对任意x∈﹙0,﹢∞﹚均成立,则f(x)单调递增;
③a>0时,f(x)在(0,$\frac{1}{a}$上单调递增,在($\frac{1}{a}$,﹢∞)上单调递减.
综上,a≤0,f(x)在﹙0,﹢∞﹚上单调递增;a>0,f(x)在(0,$\frac{1}{a}$)上单调递增,在($\frac{1}{a}$,﹢∞)上单调递减;
(2)f(x)<-2a-1=f(1)由(1)知,当a≤0时,x>1,f(x)单调递增,故f(x)>f(1)矛盾.
所以a>0,因为f(1)>f(x),可知(1,x)在f(x)递减区间,故$\frac{1}{a}$≤1<x 解得a≥1;
(3)g(x)=f(x)+(a-4)lnx+3ax-$\frac{3a+1}{x}$=-2lnx+3ax-$\frac{3a+1}{x}$,
∴g′(x)=$\frac{3a{x}^{2}-2x+(3a+1)}{{x}^{2}}$
∵g(x)在区间[1,4]上不单调,∴g(x)在[1,4]上有极值;
即方程$\frac{3a{x}^{2}-2x+(3a+1)}{{x}^{2}}$=0在[1,4]上有解,
∴3a=$\frac{2x-1}{{x}^{2}+1}$在[1,4]上有解,
构造函数h(x)=$\frac{2x-1}{{x}^{2}+1}$,x∈[1,4],则h′(x)=$\frac{2(-{x}^{2}+x+1)}{({x}^{2}+1)^{2}}$<0,
∴h(x)在[1,4]上单调递减,
∴3a∈[$\frac{7}{17}$,$\frac{1}{2}$],
∴a∈[$\frac{7}{51}$,$\frac{1}{6}$].
点评 本题考查导数知识的综合运用,考查函数的单调性,考查学生分析解决问题的能力,属于中档题.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:解答题
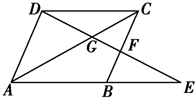 如图所示,在平行四边形ABCD中,点E是AB延长线上一点,DE交AC于点G,交BC于点F.
如图所示,在平行四边形ABCD中,点E是AB延长线上一点,DE交AC于点G,交BC于点F.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,0,0) | B. | $({\frac{{\sqrt{3}}}{4},\frac{3}{4},\frac{1}{2}})$ | C. | $({\frac{{\sqrt{3}}}{4}π,\frac{3}{4}π,\frac{π}{2}})$ | D. | $({\frac{3}{4}π,\frac{{\sqrt{3}}}{4}π,\frac{π}{2}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{\sqrt{6}}{6}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | $\frac{\sqrt{30}}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1<x<0} | B. | {x|x≥1} | C. | {x|x>0} | D. | {x|x>-1} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com