
喜欢户外运动情况 性别 | 喜欢户外运动 | 不喜欢户外运动 | 合计 |
| 男性 | 20 | ||
| 女性 | 15 | ||
| 合计 | 50 |
| P(x2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (1)根据在全部50人中随机抽取1人的概率是$\frac{3}{5}$,可得喜欢户外活动的男女员工共30人,其中男员工20人,从而可得列联表;
(2)该公司男员工抽取的概率为$\frac{25}{50}$,由此可得该公司男、女员工的人数;
(3)计算K2,与临界值比较,即可得到结论.
解答 解:(1)∵在这50人中随机抽取1人抽到喜欢户外运动的员工的概率是$\frac{3}{5}$,
∴喜欢户外活动的男女员工共30人,其中男员工20人,列联表补充如下:
| 喜欢户外运动 | 不喜欢户外运动 | 合计 | |
| 男性 | 20 | 5 | 25 |
| 女性 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
点评 本题考查概率与统计知识,考查独立性检验,正确计算是关键.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{13}{20}$ | C. | $\frac{4}{11}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
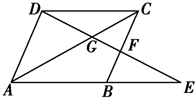 如图所示,在平行四边形ABCD中,点E是AB延长线上一点,DE交AC于点G,交BC于点F.
如图所示,在平行四边形ABCD中,点E是AB延长线上一点,DE交AC于点G,交BC于点F.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
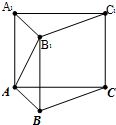
| A. | 45° | B. | 60° | C. | 30° | D. | 75° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 零件数x(个) | 10 | 20 | 30 | 40 | 50 |
| 加工时间y | 71 | 76 | 79 | 89 |
| A. | 85 | B. | 86 | C. | 87 | D. | 88 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,0,0) | B. | $({\frac{{\sqrt{3}}}{4},\frac{3}{4},\frac{1}{2}})$ | C. | $({\frac{{\sqrt{3}}}{4}π,\frac{3}{4}π,\frac{π}{2}})$ | D. | $({\frac{3}{4}π,\frac{{\sqrt{3}}}{4}π,\frac{π}{2}})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com