
| A. | 45° | B. | 60° | C. | 30° | D. | 75° |
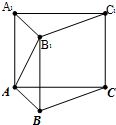
分析 取BC中点D,连接AD,B1D,则AD⊥平面BB1C1C,于是∠AB1D为所求角,设AB=$\sqrt{2}$,BB1=1,利用勾股定理计算AD,AB1得出sin∠AB1D.
解答 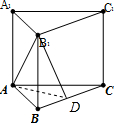 解:取BC中点D,连接AD,B1D,则AD⊥平面BB1C1C,
解:取BC中点D,连接AD,B1D,则AD⊥平面BB1C1C,
∴∠AB1D为所求角,
设AB=$\sqrt{2}$,AA1=1,则AD=$\frac{\sqrt{6}}{2}$.AB1=$\sqrt{3}$.
∴sin∠AB1D=$\frac{AD}{A{B}_{1}}$=$\frac{\sqrt{3}}{2}$.
∴∠AB1D=60°.
故选:B.
点评 本题考查了棱柱的结构特征,线面角的计算,属于中档题.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:选择题
| A. | {x|-1<x<0} | B. | $\left\{{\left.x\right|-\frac{3}{2}<x<0}\right\}$ | C. | $\left\{{\left.x\right|-\frac{5}{4}<x<0}\right\}$ | D. | {x|-2<x<0} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
喜欢户外运动情况 性别 | 喜欢户外运动 | 不喜欢户外运动 | 合计 |
| 男性 | 20 | ||
| 女性 | 15 | ||
| 合计 | 50 |
| P(x2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|1<x<2} | B. | {x|1<x<3} | C. | {x|2<x<3} | D. | {x|-1<x<3} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com