
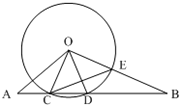
 如图,⊙O的半径为 4,线段AB与⊙O相交于点C、D,AC=2,∠BOD=∠A,OB与⊙O相交于点E.
如图,⊙O的半径为 4,线段AB与⊙O相交于点C、D,AC=2,∠BOD=∠A,OB与⊙O相交于点E.分析 (Ⅰ)由OC=OD,可得∠OCA=∠ODB.进而单调△OBD∽△AOC.利用相似三角形的性质即可得出.
(Ⅱ)由OC=OE,CE⊥OD.可得∠COD=∠BOD=∠A.进而得出.
解答 (Ⅰ)解:∵OC=OD,∴∠OCD=∠ODC,∴∠OCA=∠ODB.
∵∠BOD=∠A,∴△OBD∽△AOC.∴$\frac{BD}{OC}=\frac{OD}{AC}$,
∵OC=OD=4,AC=2,∴$\frac{BD}{4}=\frac{4}{2}$,∴BD=8.
(Ⅱ)证明:∵OC=OE,CE⊥OD.∴∠COD=∠BOD=∠A.
∴∠AOD=180°-∠A-∠ODC=180°-∠COD-∠OCD=∠ADO.
∴AD=AO.
点评 本题考查了圆的性质、相似三角形的性质、等腰三角形的性质、三角形内角和定理,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 1或-1 | D. | 以上答案都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $6\sqrt{2}$ | C. | 12 | D. | $8\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com