
分析 把第一个及第二个学校的学生看做整体,求出同校学生排在一起的方法数,再求出三个学校的学生随便排有多少种方法,由古典概型的概率计算公式得所求概率.
解答 解:由已知把第一个及第二个学校的学生看做整体得同校学生排在一起共 ${A}_{3}^{3}$${A}_{2}^{2}$${A}_{3}^{3}$种方法,
而三个学校的学生随便排有${A}_{6}^{6}$种方法,
由古典概型的概率计算公式得所求概率:
P=$\frac{{{{A}_{3}^{3}A}_{2}^{2}A}_{3}^{3}}{{A}_{6}^{6}}$=$\frac{12}{6×5×4}$=$\frac{1}{10}$,
故答案为:$\frac{1}{10}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
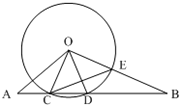 如图,⊙O的半径为 4,线段AB与⊙O相交于点C、D,AC=2,∠BOD=∠A,OB与⊙O相交于点E.
如图,⊙O的半径为 4,线段AB与⊙O相交于点C、D,AC=2,∠BOD=∠A,OB与⊙O相交于点E.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1-2i | B. | -1+2i | C. | 1+2i | D. | 1-2i |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com