
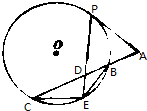
 如图,已知PA与圆O相切,P为切点,割线ABC与圆O相切于点B,C,AC=2PA,D为AC的中点.PD的延长线交圆O于E点,证明:
如图,已知PA与圆O相切,P为切点,割线ABC与圆O相切于点B,C,AC=2PA,D为AC的中点.PD的延长线交圆O于E点,证明:分析 (Ⅰ)如图3,连接PB,PC,由已知可得:∠APD=∠ADP,进而得出∠CPD=∠BPD,可得CE=EB,即可证明.
(Ⅱ)由切割线定理得,PA2=AB•AC,可得B是AD中点,由相交弦定理,得DB•DC=PD•DE,即可证明.
解答 证明:(Ⅰ)如图3,连接PB,PC,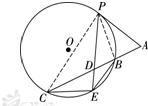
由题设知PA=AD,∴∠APD=∠ADP,
∵∠ADP=∠PCD+∠CPD,∠APD=∠BPD+∠BPA,∠PCD=∠BPA,
∴∠CPD=∠BPD,
从而$\widehat{CE}=\widehat{EB}$,因此CE=EB,
∴∠ECD=∠EBD.
(Ⅱ)由切割线定理得,PA2=AB•AC,
∵PA=AD=DC,∴DC=2AB,∴AB=DB,即B是AD中点,
由相交弦定理,得DB•DC=PD•DE,
∴2DB2=PD•DE.
点评 本题考查了圆的性质、三角形外角定理、切割线定理与相交弦定理,考查了推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $\sqrt{2}$ | C. | 2 | D. | $2\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数F(x)=$\frac{f(x)}{x}$在(0,+∞)上为增函数 | B. | 函数F (x)=$\frac{f(x)}{x}$在(0,+∞)上为减函数 | ||
| C. | 函数G(x)=xf(x)在(0,+∞)上为增函数 | D. | 函数G(x)=xf(x)在(0,+∞)上为减函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
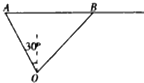 某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口O北偏西30°且与该港口相距20海里的A处,并正以30海里/小时的航行速度沿正东方向匀速行驶,经过t小时与轮船相遇.
某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口O北偏西30°且与该港口相距20海里的A处,并正以30海里/小时的航行速度沿正东方向匀速行驶,经过t小时与轮船相遇.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com