
分析 (1)利用sin2α+cos2α=1对已知函数进行变形,然后利用配方法来求函数的最大值;
(2)根据二次根式的被开方数是非负数和对数函数定义域进行计算即可.
解答 解:(1)y=cos2α+sinα+3,
=1-sin2α+sinα+3,
=-(sinα-$\frac{1}{2}$)2+$\frac{17}{4}$.
当sinα=$\frac{1}{2}$时,y最大值=$\frac{17}{4}$.
(2)依题意得:$\left\{\begin{array}{l}{2si{n}^{2}x+3sinx-2≥0}\\{-{x}^{2}+7x+8>0}\end{array}\right.$,
整理,得
$\left\{\begin{array}{l}{(sinx+2)(2sinx-1)≥0}\\{(x-8)(x+1)<0}\end{array}\right.$,
所以$\left\{\begin{array}{l}{sinx≥\frac{1}{2}}\\{-1<x<8}\end{array}\right.$.
所以x∈[$\frac{π}{6}$,$\frac{5π}{6}$]∪[$\frac{13π}{6}$,8].
点评 本题考查了函数的定义域及其求法,三角函数的最值.考查转化思想以及计算能力.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 向右平移$\frac{π}{3}$个单位,再把各点的纵坐标伸长到原来的3倍(横坐标不变) | |
| B. | 向右平移$\frac{π}{6}$个单位,再把各点的纵坐标缩短到原来的3倍(横坐标不变) | |
| C. | 向左平移$\frac{π}{3}$个单位,再把各点的纵坐标缩短到原来的3倍(横坐标不变) | |
| D. | 向左平移$\frac{π}{6}$个单位,再把各点的纵坐标伸长到原来的3倍(横坐标不变) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-4] | B. | [4,+∞) | C. | (-∞,-4]∪[4,+∞) | D. | (-∞,-4)∪(4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
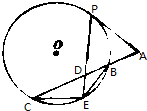 如图,已知PA与圆O相切,P为切点,割线ABC与圆O相切于点B,C,AC=2PA,D为AC的中点.PD的延长线交圆O于E点,证明:
如图,已知PA与圆O相切,P为切点,割线ABC与圆O相切于点B,C,AC=2PA,D为AC的中点.PD的延长线交圆O于E点,证明:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com