
分析 (Ⅰ)利用导数判断函数的单调性即可;
(Ⅱ)由题意得恒有ma-f(x)>a2成立,等价于ma-a2>f(x)max,利用导数求得函数的最大值,即可得出结论.
解答 解:(Ⅰ)f′(x)=2ax+$\frac{2}{x}$=$\frac{2a{x}^{2}+2}{{x}^{2}}$,(x>0),
①当a≥0时,恒有f′(x)>0,则f(x)在(0,+∞)上是增函数;
②当a<0时,当0<x<$\sqrt{-\frac{1}{a}}$时,f′(x)>0,则f(x)在(0,$\sqrt{-\frac{1}{a}}$)上是增函数;
当x>$\sqrt{-\frac{1}{a}}$时,f′(x)<0,则f(x)在($\sqrt{-\frac{1}{a}}$,+∞)上是减函数,
综上,当a≥0时,f(x)在(0,+∞)上是增函数;当a<0时,f(x)在(0,$\sqrt{-\frac{1}{a}}$)上是增函数,f(x)在($\sqrt{-\frac{1}{a}}$,+∞)上是减函数.
(Ⅱ)由题意知对任意a∈(-4,-2)及x∈[1,3]时,
恒有ma-f(x)>a2成立,等价于ma-a2>f(x)max,
因为a∈(-4,-2),所以$\frac{1}{2}$<$\sqrt{-\frac{1}{a}}$<$\frac{\sqrt{2}}{2}$<1,
由(Ⅰ)知:当a∈(-4,-2)时,f(x)在[1,3]上是减函数
所以f(x)max=f(1)=2a,
所以ma-a2>2a,即m<a+2,
因为a∈(-4,-2),所以-2<a+2<0
所以实数m的取值范围为m≤-2
点评 本题主要考查利用导数判断函数的单调性及求函数的最值知识,考查恒成立问题的等价转化思想及分类讨论思想的运用能力,属难题.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
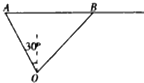 某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口O北偏西30°且与该港口相距20海里的A处,并正以30海里/小时的航行速度沿正东方向匀速行驶,经过t小时与轮船相遇.
某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口O北偏西30°且与该港口相距20海里的A处,并正以30海里/小时的航行速度沿正东方向匀速行驶,经过t小时与轮船相遇.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,+∞) | B. | [2,+∞) | C. | (-1,+∞) | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -20 | B. | -15 | C. | 15 | D. | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com