
分析 设出伸缩变换公式,代入直线方程,即可求出变换公式.
解答 解:设伸缩变换公式为$\left\{\begin{array}{l}{x′=ax}\\{y′=by}\end{array}\right.$,
∴$\left\{\begin{array}{l}{x=\frac{1}{a}x′}\\{y=\frac{1}{b}y′}\end{array}\right.$.
代入x+y+2=0得$\frac{1}{a}x′$+$\frac{1}{b}$y′+2=0,
∴$\frac{1}{a}$:8=$\frac{1}{b}$:1=2:8,
解得a=$\frac{1}{2}$,b=4.
故答案为$\left\{\begin{array}{l}{x′=\frac{1}{2}x}\\{y′=4y}\end{array}\right.$.
点评 本题考查了坐标变换,属于基础题.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:解答题
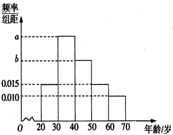 根据微信同程旅游的调查统计显示,参与网上购票的1000位购票者的年龄(单位:岁)情况如图所示.
根据微信同程旅游的调查统计显示,参与网上购票的1000位购票者的年龄(单位:岁)情况如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
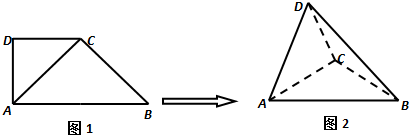
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向右平移$\frac{π}{3}$个单位,再把各点的纵坐标伸长到原来的3倍(横坐标不变) | |
| B. | 向右平移$\frac{π}{6}$个单位,再把各点的纵坐标缩短到原来的3倍(横坐标不变) | |
| C. | 向左平移$\frac{π}{3}$个单位,再把各点的纵坐标缩短到原来的3倍(横坐标不变) | |
| D. | 向左平移$\frac{π}{6}$个单位,再把各点的纵坐标伸长到原来的3倍(横坐标不变) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
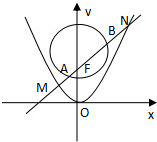 已知点F是抛物线C:x2=2py(p>0)的焦点,点P(3,y0)(y0>1)是抛物线C上一点,且$|{PF}|=\frac{13}{4}$,⊙Q的方程为x2+(y-3)2=6,过点F作直线l,与抛物线C和⊙Q依次交于M,A,B,N.(如图所示)
已知点F是抛物线C:x2=2py(p>0)的焦点,点P(3,y0)(y0>1)是抛物线C上一点,且$|{PF}|=\frac{13}{4}$,⊙Q的方程为x2+(y-3)2=6,过点F作直线l,与抛物线C和⊙Q依次交于M,A,B,N.(如图所示)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
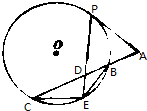 如图,已知PA与圆O相切,P为切点,割线ABC与圆O相切于点B,C,AC=2PA,D为AC的中点.PD的延长线交圆O于E点,证明:
如图,已知PA与圆O相切,P为切点,割线ABC与圆O相切于点B,C,AC=2PA,D为AC的中点.PD的延长线交圆O于E点,证明:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com