
分析 (1)令f'(2)=0,解得a,再验证是否符合函数取得极值的充分条件即可;
(2)对a分类讨论,利用导数与函数单调性的关系即可得出;
(3)通过讨论a的范围,求出函数的单调区间,结合题意求出a的范围即可.
解答 解:(1)f′(x)=$\frac{x(1-a-ax)}{x+1}$,x∈(-1,+∞)
依题意,令f'(2)=0,解得a=$\frac{1}{3}$,
经检验,当a=$\frac{1}{3}$时,x=2是f(x)的极值点.
∴a=$\frac{1}{3}$;
(2)①当a=0时,f′(x)=$\frac{x}{x+1}$,
故f(x)的单调增区间是(0,+∞);单调减区间是(-1,0).
②当a>0时,令f'(x)=0,得x1=0,或x2=$\frac{1}{a}$-1,
当0<a<1时,f(x)与f'(x)的情况如下:
| x | (-1,x1) | x1 | (x1,x2) | x2 | (x2,+∞) |
| f'(x) | - | 0 | + | 0 | - |
| f(x) | ↘ | f(x1) | ↗ | f(x2) | ↘ |
| x | (-1,x2) | x2 | (x2,x1) | x1 | (x1+∞) |
| f'(x) | - | 0 | + | 0 | - |
| f(x) | ↘ | f(x2) | ↗ | f(x1) | ↘ |
点评 熟练掌握利用导数研究函数的单调性、极值、分类讨论的思想方法等是解题的关键.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
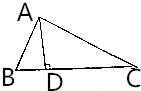 △ABC中,AD⊥BC,且$\frac{1}{A{C}^{2}}$=$\frac{1}{A{D}^{2}}$-$\frac{1}{A{B}^{2}}$,求证:△ABC是直角三角形.
△ABC中,AD⊥BC,且$\frac{1}{A{C}^{2}}$=$\frac{1}{A{D}^{2}}$-$\frac{1}{A{B}^{2}}$,求证:△ABC是直角三角形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{6+3\sqrt{3}}{4}$ | B. | $\frac{3+\sqrt{3}}{3}$ | C. | $\frac{5}{4}$ | D. | $\frac{9}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{27}$ | B. | $\frac{8}{27}$ | C. | $\frac{4}{9}$ | D. | $\frac{8}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{3\sqrt{2}}{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com